What Is the Velocity of the Krypton Atom Relative to the Tube?

[Man1la]

Homework Statement

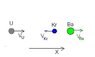
A uranium atom (U), traveling with a velocity of 5.00 x 10^5 m/s relative to the containing tube breaks up into krypton (Kr) and barium (Ba). The krypton atom is ejected directly backwards at a velocity of 2.35 x 10^6 m/s relative to the barium after separation. With what velocity does the barium atom move forward relative to the tube? You may assume no other particles are produced, and that relativistic corrections are small.

What is the velocity of the krypton atom relative to the containing tube? (Kr = 95.0; Ba = 140; U = 235 u)

Homework Equations

Conservation of linear momentum.

The Attempt at a Solution

The relative velocity factor is really confusing me on this question. I'm not sure how to incorporate this into general conservation of linear momentum equations. The answer should be 1.46 x 10^6 m/s but I got 2.43 x 10^6 m/s. I have tried a number of different approaches but can't get to the correct answer. Can anyone point me in the right direction please?

Thanks a lot

 

[Man1la]

Sorry, it is the first part "With what velocity does the barium atom move forward relative to the tube?" which I am trying to solve.

 

[cepheid]

Welcome to PF,

There are a number of different ways of solving this problem, but I find it easiest to start in the rest frame of the uranium atom. In other words, consider the uranium atom to be stationary, and the tube is moving backwards past it at v_tube = -5.00 (I omit factors of 10^5 m/s in my velocity numbers for simplicity, you can put them back in).

Now, the uranium atom suddenly splits up into Kr and Ba atoms, with the Kr moving backwards and the Ba moving forwards. Since we started with the uranium atom at rest, conservation of momentum in this frame is just m_Kv_K = -m_Bv_B, where these velocities are still measured relative to the original rest frame of the U atom.

However, our Kr velocity isn't given relative to the U atom, it's given relative to the barium atom. It sounds like this problem wants you to ignore the effects of special relativity. This means that we can change reference frames using the Galilean transformation instead of the Lorentz transformation. In other words, to change from one reference frame to another, just ADD relative velocities. For example, to change to the rest frame of the Ba atom, just subtract v_B from all velocities. So, the barium atom speed in its own frame is v_B - v_B = 0. Relative to the forward moving Ba atom, the tube is receding even faster at -5.00 - v_B. And the problem is telling you that v_K - v_B (speed of Kr relative to Ba) = -23.5.

Given these two equations in bold, can you take it from here?

EDIT: once you solve for v_K and v_B using these equations, these will be the speeds measured in the original rest frame of the U atom. You will have to transform back to the rest frame of the tube to get your final answer.

 

[ehild]

https://www.physicsforums.com/attachment.php?attachmentid=63688&d=1383719144

See Figure. It shows the velocities with respect to the tube .
Relative velocity of Kr with respect to Ba is V(rel) = V_Kr-V_Ba. As the Kr atom is ejected backwards from the Uranium, and the Ba is ejected forward, the velocity of the Kr is less than that of the Ba, so its relative velocity is negative.

V(rel) = V_Kr-V_Ba= -2.35 x 10^6 m/s. That means

V_Kr=V_Ba -2.35 x 10^6 .

Write up the equation for conservation of momentum and solve for V_Ba.

ehild

 

[j_namtirach]

Thank you for the help guys.

I solved the problem quite easily using the second explanation from ehild.

Cepheid, your explanation seems to be a more detailed description of how the Galilean transformation can be used in these situations. I will try to work on this. I have to admit I didn't manage to solve the problem using your method though. I ended up going around in circles a bit and wasn't able to get an appropriate value for the velocity of Barium. Please could you show me how to reach the answer with your method, as I'm still a little confused about how you use it.

Thanks you both

 

[cepheid]

Thank you for the help guys.

I solved the problem quite easily using the second explanation from ehild.

Cepheid, your explanation seems to be a more detailed description of how the Galilean transformation can be used in these situations. I will try to work on this. I have to admit I didn't manage to solve the problem using your method though. I ended up going around in circles a bit and wasn't able to get an appropriate value for the velocity of Barium. Please could you show me how to reach the answer with your method, as I'm still a little confused about how you use it.

Thanks you both

If you were the OP (original poster), then I would be happy to provide the help you have requested, provided that you showed your attempt at a solution. At PF, we do not do other people's homework for them, but if you make a solid attempt, then we are happy to point out where you went wrong, and provide assistance to help you solve it.

However, I notice that you are not the OP. Your post made it sound like you were, suggesting to me that you are trying to trick unobservant people into helping you with this problem. Generally speaking, it's bad form to hijack other people's threads. However, the same condition applies: if you show us what you've done so far on this problem, I'll be willing to help point you in the right direction.

Regards,

cepheid

EDIT 1: ehild's method is exactly the same as mine, except that he does it in different reference frame, which means the total momentum of the system is different.

EDIT 2: My first post may have been a bit verbose, but it provided two equations (in boldface) for you to use. So I thought that this was quite straightforward.

EDIT 3: ehild, your figure doesn't show up for me.

 

[ehild]

I tried to apply the method to copy the PF URL of the picture into my post

Do you see the picture in the text now?

I used the laboratory frame of reference, velocities with respect to the tube. Anyway, the velocity of Kr with respect to the Ba is the same in both frames of reference: $\vec V_{rel} =\vec V_{Kr}-\vec V_{Ba}$

As far as I know, anybody can use the hints in the threads, not only the OP-s. It is not "hijacking other people's thread". And anybody can write a comment in any thread. Maybe, I am wrong and you know it better, as you are a Mentor. Have I also hijacked your post, giving my hint as I considered your method a bit confusing for the OP, a newcomer?

ehild

 

[Man1la]

Hi guys,

Sorry about the misunderstanding here but I was at my school computer yesterday and had forgotten my password for the forum so created a new account so that I could post. I didn't think when I got home and used my home computer. I'm automatically logged on on that and that is why the other username came up. Sorry about that. There was no intention to deceive.

Here is how I solved the problem using ehild's method. I'm afraid I'm not familiar with how to use the correct notation on this so I have presented it in the clumsy format below:

235 x (5 x 10^5) = 95(vba - (2.35 x 10^6)) + 140vba

1.175 x 10^8 = 95vba - (2.23 x 10^8) + 140vba

3.41 x 10^8 = 235vba

vba = 1.45 x 10^6 m/s

I didn't mean to criticize your explanation at all Cepheid. Sorry if it came across that way. I'm really grateful for such a thorough explanation. You did include two equations to use, quite clearly. I have worked on it again and have almost got it, although I'm not sure of the significance of the first bold equation you gave, and I seem to have negative value where I should have a positive. I'll work out where I went wrong eventually I'm sure!

95vkr = -140vba

-(1.175 x 10^8) - 235vba = 95(vkr - vba)

-1.175 x 10^8 - 235vba = -2.23 x 10^8

235vba = 1.06 x 10^8

vba = 4.49 x 10^5 m/s

Thank you both for your help.

 

[ehild]

Hi guys,

Sorry about the misunderstanding here but I was at my school computer yesterday and had forgotten my password for the forum so created a new account so that I could post. I didn't think when I got home and used my home computer. I'm automatically logged on on that and that is why the other username came up. Sorry about that. There was no intention to deceive.

Here is how I solved the problem using ehild's method. I'm afraid I'm not familiar with how to use the correct notation on this so I have presented it in the clumsy format below:

235 x (5 x 10^5) = 95(vba - (2.35 x 10^6)) + 140vba

1.175 x 10^8 = 95vba - (2.23 x 10^8) + 140vba

3.41 x 10^8 = 235vba

vba = 1.45 x 10^6 m/s

It is correct.

I didn't mean to criticize your explanation at all Cepheid. Sorry if it came across that way. I'm really grateful for such a thorough explanation. You did include two equations to use, quite clearly. I have worked on it again and have almost got it, although I'm not sure of the significance of the first bold equation you gave, and I seem to have negative value where I should have a positive. I'll work out where I went wrong eventually I'm sure!

95vkr = -140vba

-(1.175 x 10^8) - 235vba = 95(vkr - vba)
-1.175 x 10^8 - 235vba = -2.23 x 10^8

I do not understand your equation. VBa and Vkr are opposite in that system, so Vkr is negative.

Better to use an other letter in this frame of reference, say U.

So

95 Ukr = -140 Uba and Ukr-Uba=-235 x10₆


"Galilean transformation" means that you add velocities as vectors. If you walk forward in a train with 2m/s and the train travels with 28 m/s, your velocity is 28+2=30 m/s with respect to the ground. When you walk backwards in the train, your velocity is 28-2=26 m/s with respect to the ground.

When the Uranium atom splits into two, the centre of mass of the particles moves with the original velocity of the Uranium. In principle, you use a centre-of mass frame of reference when working velocities with respect to the Uranium. In the CoM frame, the net momentum is zero.

When you have the velocities in the CoM frame of reference, just add the velocity of the CoM to get the velocities in the rest frame of reference.

If you solved the equations for UBa, adding the original velocity of Uranium (5.00 x 10^5 m/s) gives the answer.


ehild

 

[cepheid]

As far as I know, anybody can use the hints in the threads, not only the OP-s. It is not "hijacking other people's thread". And anybody can write a comment in any thread. Maybe, I am wrong and you know it better, as you are a Mentor. Have I also hijacked your post, giving my hint as I considered your method a bit confusing for the OP, a newcomer?

ehild

Ehild,

You appear to have taken offence where none was intended, sorry. Allow me to clarify my position. Of course anyone can write any comment in any thread, as long as it is not in violation of the PF rules. And of course, it is reasonable for a second person working on the exact same problem as the OP to join the discussion in that thread. So, saying that this was an example thread hijacking may have been overstating things somewhat. My point was this: if j_namtirach had actually been a second distinct person, then I would have required him/her to join the thread by saying something along the lines of this:

"Hey guys, I'm working on the same problem as the OP, and using the hints that you gave him, I made the following attempt at a solution: (insert attempt at solution here). However, I'm still having trouble/not getting the right answer. Can you help me figure out where I'm going wrong?"

Without this presentation of some attempt at a solution, we cannot explicitly offer this second person help. He/she can continue to benefit from help that we give to the OP in the thread, but we cannot provide answers to specific questions asked by him (and not the OP) unless if he is making some effort solve it on his own. Those are the PF rules as I interpret them.

In this case, it turned out that the second username did not belong to a distinct person, but rather the OP, so it's all good.

 

[ehild]

Well, I am usually at the side of the kids asking for help, and rise my word when I notice cruelty in an answer.
A newcomer may behave not exactly as you would expect. Explain him what he did wrong before condemning him.

ehild

 

[Bharat Oli98086]

Velocity of uranum w.r.t tube(V1)=5×10^5
Velocity of krypton with respect to barium (V2)=2.35×10^6
U=235
Ba=140
Kr=95
Velocity of Barium w.r.t tube (V3)=?
Velocity of krypton w.r.t tube (V4)=?

We have,
V2 = V3 +V4
or, 2.35×10^6=V3+V4
or,V3=(2.35×10^6)-V4

Also,
Initial linear momentum of uranium=Final linear momentum of Barium and krypton
or,U×5×10^5=(Ba×V3)-(Kr×V4)
or,235×5×10^5={140×(2.35×10^6-V4)}-(95×V4)
or,1175×10^5=(329×10^6-140V4)-95V4
or,235V4=211.5×10^6
or,V4=9×10^5

Again,
V3=(2.35×10^6-9×10^5)
or,V3=1.45×10^6

[Mentor Note -- Complete solution allowed because this thread is so old and the OP had solved the problem for themselves]