What is the Voltage Output in a Complex Network Using KCL and Voltage Dividers?

[STEMucator]

I was able to do most of the exercises, but this one gave me some trouble. I want to find $V_o$.

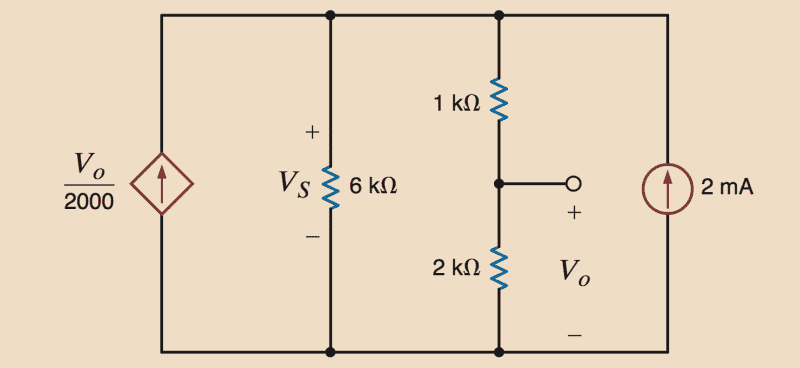
My gut is telling me to use KCL, and applying it to the top left node above the 6k resistor yields:

$\frac{V_o}{2000} + 2 \times 10^{-3} - \frac{V_s}{6000} - \frac{V_s}{3000} = 0$

I am now somewhat unsure how to proceed. I know the potential across the branches is $V_s$.

 

[gneill]

Write another equation for the branch with the two resistors and Vo. The equation should relate Vo to the voltage Vs (the voltage of the node). Then you'll have something to replace Vo in your node equation, leaving you with just one unknown.

 

[STEMucator]

Write another equation for the branch with the two resistors and Vo. The equation should relate Vo to the voltage Vs (the voltage of the node). Then you'll have something to replace Vo in your node equation, leaving you with just one unknown.

I suspected I was trying to relate $V_s$ and $V_o$, but I can't see it for some reason. Probably due to hunger. Applying KVL didn't seem to give me anything useful, so I'm still a bit unsure what to do.

 

[STEMucator]

The only equation I can see is: $V_s = V_o + V_x$ where $V_x$ is the voltage across the 1k.

 

[gneill]

The potential at the top node is $V_s$. That branch with $V_o$ looks like a voltage divider to me... ;)

 

[STEMucator]

The potential at the top node is $V_s$. That branch with $V_o$ looks like a voltage divider to me... ;)

I can't believe I forgot entirely about voltage dividers.

So I guess I could just say that $V_o = [\frac{2k}{1k + 2k}]V_s = \frac{2}{3} V_s$

Subbing this into the KCL equation gives $V_s = 12 V$, which then subbing back gives $V_o = 8 V$.

I'm going to go eat now, thank you.