- #1
- 2,168
- 193
Problem:
Here’s a little Monte Carlo challenge problem, Consider the following game, which uses the two spinner disks. Suppose a player spins one or the other of the pointers on the disks according to the following rules: (1) if the player spins pointer ##i## and it stops in the region with area ##p_{ij}##, he moves from disk ##i## to disk ##j## (i and j are either 1 or 2); (2) if a pointer stops in the region with area ##x_i##, the game ends; (3) if the game ends in the region with area ##x_1##, the player wins, but if the pointer stops in the region with area ##x_2## the player loses. What is the probability the player, starting with disk 1, wins? Assume the area of each disk is one, so that ##x_1+p_{11}+p_{12} =1##, as well as that ##x_2+p_{21}+p_{22} =1##
Run your code for the case of ##p_{11} =0.2, p_{12} =0.4, p_{21} =0.3##, and ##p_{22} =0.35##.
Mentor note: Changed ICODE tags to code=python
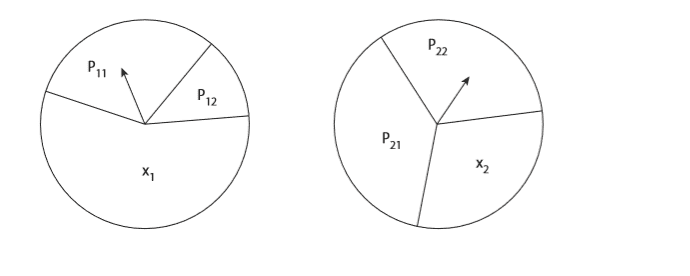
The correct answer is 0.5821 however I am getting 0.655.. Where am I doing wrong ?
Here’s a little Monte Carlo challenge problem, Consider the following game, which uses the two spinner disks. Suppose a player spins one or the other of the pointers on the disks according to the following rules: (1) if the player spins pointer ##i## and it stops in the region with area ##p_{ij}##, he moves from disk ##i## to disk ##j## (i and j are either 1 or 2); (2) if a pointer stops in the region with area ##x_i##, the game ends; (3) if the game ends in the region with area ##x_1##, the player wins, but if the pointer stops in the region with area ##x_2## the player loses. What is the probability the player, starting with disk 1, wins? Assume the area of each disk is one, so that ##x_1+p_{11}+p_{12} =1##, as well as that ##x_2+p_{21}+p_{22} =1##
Run your code for the case of ##p_{11} =0.2, p_{12} =0.4, p_{21} =0.3##, and ##p_{22} =0.35##.
Mentor note: Changed ICODE tags to code=python
Python:
import random
p_11 = 0.2
p_12 = 0.4 #0.2+0.4
p_21 = 0.3
p_22 = 0.35 P_1 = p_11+p_12
P_2 = p_21+p_22 #from starting 1:
wins = 0
num = 0
for i in range(10**7):
while num < P_1:
num = random.uniform(0,1)
if P_1 < num < 1: #area corresponding to x_1
wins += 1 #wins
num = 0
break
else:
num2 = random.uniform(0,1)
if P_2 < num2 < 1: #area corresponding to x_2
break #loses
print(wins/10**7)
Last edited: