- #1
operationsres
- 103
- 0
Hi,
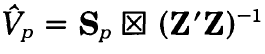
A fuller view can be found here:

(i) What is this operator?
(ii) What does this operator mean if Sp is a 5x5 matrix and (Z'Z)-1 is a 3x3 matrix?Thanks a lot.
A fuller view can be found here:
(i) What is this operator?
(ii) What does this operator mean if Sp is a 5x5 matrix and (Z'Z)-1 is a 3x3 matrix?Thanks a lot.
Last edited: