What is wrong in this 2nd order transfer function?

[cnh1995]

Homework Statement

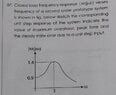
Find the parameters mentioned in the problem statement image i.e. peak time, peak overshoot, steady state error for unit step input.

Relevant Equations

Standard second order system transfer function.

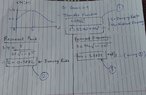
I have attached my attempt at a solution.
In the solution image, I have computed 3 things:
1. System transfer function based on my understanding of the problem statement.
This is a 2nd order system with steady state dc gain=0.9. So I wrote the transfer function accordingly.
However, I strongly feel it is incorrect since this is not a "standard" 2nd order system anymore as the dc gain isn't 1. So I am not sure if I have modified the transfer function correctly to account for this dc gain of 0.9.

2. Damping ratio z: This I have computed again using the formula for "standard" 2nd order system's frequency response. But if the transfer function itself is incorrect, I feel this calculation is too.

3. Natural frequency: Same as 2.

How do I correctly account for this 0.9 dc gain and write the correct transfer function? What am I missing here? (Whatever it is, I am sure it's pretty fundamental).
Once I write the correct transfer function, other parameters can be computed easily.

Any help is appreciated!

 

[LvW]

I have found your question only today (3 weeks after it was posred).
Question: Are you still interested in an answer?

 

[cnh1995]

I have solved this question, and got all answers correctly finally.
Turns out there is nothing wrong with my transfer function. Actually, the resonant peak formula that I used is wrong for this particular problem. It should have 0.9 in the numerator instead of 1.
Thanks @LvW for your interest!