zenterix
- 774
- 84
- Homework Statement
- Consider the non-homogeneous 2nd order linear differential equation with constant coefficients and sinusoidal input
$$y''+py'+qy=a_1\sin{bx}+a_2\cos{bx}$$
- Relevant Equations
- Note that the characteristic equation for the homogeneous equation is
$$r^2+pr+q=0\tag{1}$$
with discriminant
$$\Delta = p^2-4q\tag{2}$$
If ##p^2-4q<0## then we know that the homogeneous equation has a general solution
$$y_g(x)=c_1\sin{kx}+c_2\cos{kx}\tag{3}$$
where
$$k=\frac{1}{2}\sqrt{-\Delta}=\frac{\sqrt{4q-p^2}}{2}\tag{4}$$
Suppose we guess at a solution ##y_p## to the non-homogeneous equation
$$y_p(x)=A\sin{bx}+B\cos{bx}\tag{5}$$
If
$$b=k=\frac{\sqrt{4q-p^2}}{2}\tag{6}$$
then as far as I can tell, this guess should not work since subbing it into the nonhomogeneous equation should make the left-hand side identically zero, which is not equal to the sinusoidal input for all ##x##.
My question is if the reasoning above is correct. In particular, if (6) is indeed the condition that makes the above guess of ##y_p## fail.
I am asking because I have tried subbing (5) into the homogeneous equation the left-hand side doesn't seem to come out to zero.
Here is what I mean
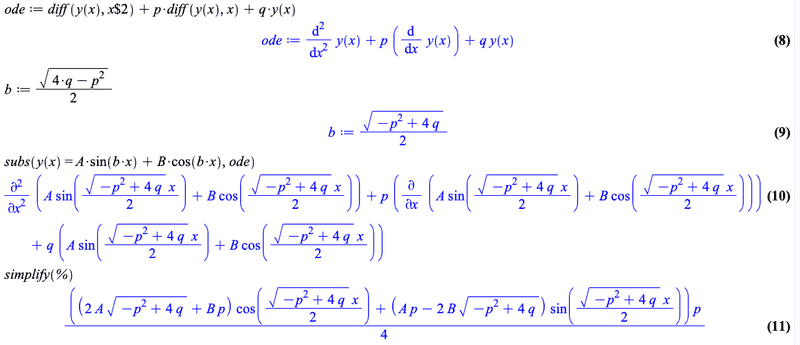
Now, I straight up subbed in ##y_p## into the original differential equation without imposing any conditions.
However, in the final expression above, namely (11), it isn't clear at all what is required to make the expression zero.
$$y_g(x)=c_1\sin{kx}+c_2\cos{kx}\tag{3}$$
where
$$k=\frac{1}{2}\sqrt{-\Delta}=\frac{\sqrt{4q-p^2}}{2}\tag{4}$$
Suppose we guess at a solution ##y_p## to the non-homogeneous equation
$$y_p(x)=A\sin{bx}+B\cos{bx}\tag{5}$$
If
$$b=k=\frac{\sqrt{4q-p^2}}{2}\tag{6}$$
then as far as I can tell, this guess should not work since subbing it into the nonhomogeneous equation should make the left-hand side identically zero, which is not equal to the sinusoidal input for all ##x##.
My question is if the reasoning above is correct. In particular, if (6) is indeed the condition that makes the above guess of ##y_p## fail.
I am asking because I have tried subbing (5) into the homogeneous equation the left-hand side doesn't seem to come out to zero.
Here is what I mean
Now, I straight up subbed in ##y_p## into the original differential equation without imposing any conditions.
However, in the final expression above, namely (11), it isn't clear at all what is required to make the expression zero.
Last edited: