songoku
- 2,485
- 393
- Homework Statement
- Draw the graph of ##F=-2x## and calculate the work done from ##[-1,1]##
- Relevant Equations
- Work = area under the graph
The answer key is zero because the areas are above and below x-axis and have equal magnitude so canceling out each other.
But I am confused about the solution
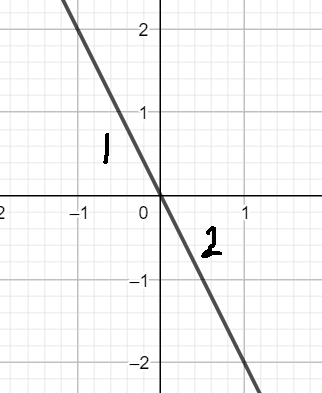
Area 1 is above x-axis but I think the work done is negative since the sign of ##F## and ##x## is opposite. Work done on area 2 is also negative for the same reasoning so my answer would be -2 J
Where is my mistake? Thanks
But I am confused about the solution
Area 1 is above x-axis but I think the work done is negative since the sign of ##F## and ##x## is opposite. Work done on area 2 is also negative for the same reasoning so my answer would be -2 J
Where is my mistake? Thanks