migyonne
- 8
- 0
Hello and thank you for welcoming me to your forum!
To get started, I would like to give you a little help:
In the pattern experiment, when firing the cannon,
if part of the momentum reaches the bird,
and if another part of the momentum manages to stun the fish,
what part of the momentum would be likely to make the boat move?
It seems that there is no example on the internet... nor in physical science books...
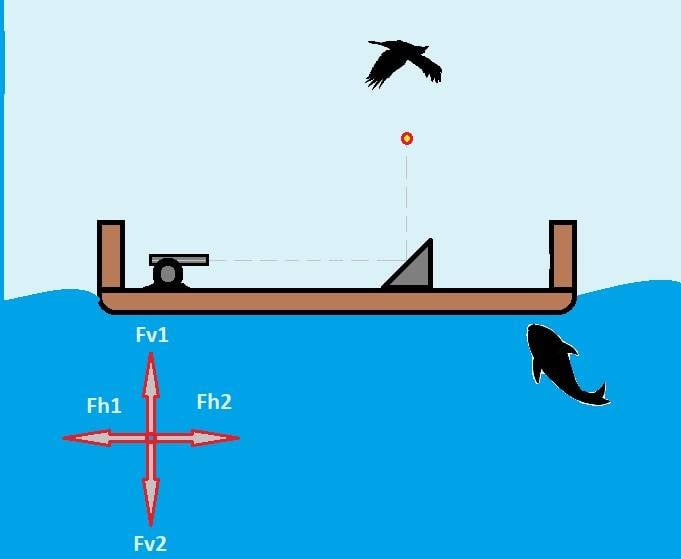
To get started, I would like to give you a little help:
In the pattern experiment, when firing the cannon,
if part of the momentum reaches the bird,
and if another part of the momentum manages to stun the fish,
what part of the momentum would be likely to make the boat move?
It seems that there is no example on the internet... nor in physical science books...
