What Power Is Needed To Accelerate An Object To 2.7 rad/s In 5.2 s?

AI Thread Summary
To determine the power needed to accelerate an object to an angular speed of 2.7 rad/s in 5.2 seconds, the relevant equation is P = W / t, where W represents work. The correct approach involves calculating the rotational kinetic energy (KE) at the target angular velocity, using the formula KE = 0.5 * I * ω², where I is the moment of inertia. The user initially struggled with finding acceleration and applied the wrong motion equation, leading to an incorrect result. Ultimately, the required power to achieve the desired acceleration is 1.3 W. Understanding the relationship between power, work, and kinetic energy is crucial for solving this problem.
n.hirsch1
Messages
13
Reaction score
0

Homework Statement


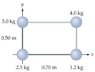
See the image attached
What power must be applied to this object to accelerate it from rest to an angular speed of 2.7 rad/s in 5.2 s about the x axis?


Homework Equations


P = W / t - torque * angular velocity


The Attempt at a Solution


P = [(0.5 m)*(7 kg)*(acceleration)] * 2.7 rad/s
I don't know how to find acceleration or if I am doing this wrong all together. The right answer is 1.3 W. I tried plugging it into the motion equation v = vo + at to get a, that gave me the wrong answer.
 

Attachments

  • Walker4e.ch11.Pr083.jpg
    Walker4e.ch11.Pr083.jpg
    6.2 KB · Views: 500
Physics news on Phys.org
The work goes into making the system have kinetic energy. Your starting point should be P = KE/time. Now you just have to figure out how much rotational kinetic energy it has when ω = 2.7 rad/s.
 

Thread 'Errors and significant figures'

I multiplied the values first without the error limit. Got 19.38. rounded it off to 2 significant figures since the given data has 2 significant figures. So = 19. For error I used the above formula. It comes out about 1.48. Now my question is. Should I write the answer as 19±1.5 (rounding 1.48 to 2 significant figures) OR should I write it as 19±1. So in short, should the error have same number of significant figures as the mean value or should it have the same number of decimal places as...
View full post »
Thread 'A cylinder connected to a hanging mass'

Thread 'A cylinder connected to a hanging mass'

Let's declare that for the cylinder, mass = M = 10 kg Radius = R = 4 m For the wall and the floor, Friction coeff = ##\mu## = 0.5 For the hanging mass, mass = m = 11 kg First, we divide the force according to their respective plane (x and y thing, correct me if I'm wrong) and according to which, cylinder or the hanging mass, they're working on. Force on the hanging mass $$mg - T = ma$$ Force(Cylinder) on y $$N_f + f_w - Mg = 0$$ Force(Cylinder) on x $$T + f_f - N_w = Ma$$ There's also...
View full post »

Similar threads

Finding linear acceleration of a spool and cable
Replies
6
Views
2K
Centripetal Acceleration while Swinging a Stone on a String
Replies
9
Views
1K
How to calculate angular speed?
Replies
7
Views
2K
What is the angular speed of the rollers after 1.14 s?
Replies
2
Views
1K
Angular Acceleration: 0.29 rad/s/s
Replies
2
Views
2K
Determine the angular acceleration and angular velocity
Replies
2
Views
3K
Angular Acceleration Homework: 962 Revolutions in 10 Secs
Replies
1
Views
4K
Therefore, the angular acceleration is 3.925 rad/s2.
Replies
2
Views
2K
Angular Velocity & Acceleration for a Series of Connected Objects
Replies
1
Views
2K
Solving angular acceleration Problem
Replies
5
Views
2K

Hot Threads

Recent Insights

Back
Top