ssafdarpk
- 1
- 0
Can someone help me understand the answer to this differential?
I have the following expression
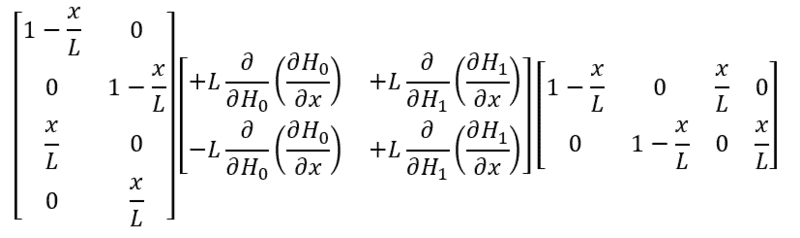 where
where
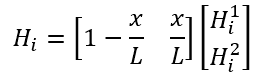
Now what I can understand the differential of
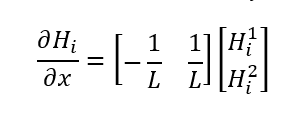
what will be the following?

I have the following expression
Now what I can understand the differential of
what will be the following?