Finding acceleration of blocks A and B in pulley system

[Adesh]

Homework Statement

Find the acceleration of block A and block B.

Relevant Equations

$F=ma$.

Find the acceleration of block A and B, given that the mass of pulleys and strings are negligible.

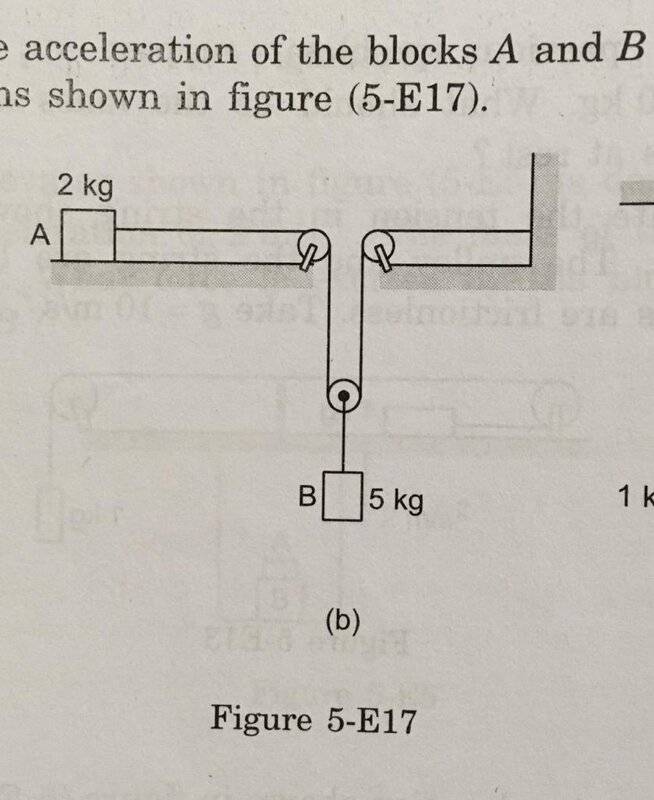. I could see that the block B has gravity acting on it, therefore the gravitational force on the block $B$ is $F_B = 5 g$ and hence the acceleration is $g$. From the pulley to which block B is connected there goes two strings, therefore tension on each string will be half of $F_B$, therefore the force on the block $A$ is $F_A = \frac{F_B}{2} = \frac{5g}{2}$ and therefore the acceleration of the block $A$ is $\frac{5g}{4}$. Unfortunately, my answers are wrong, the correct answers are $\text{acceleration of block A}= \frac{2}{7} g$ and $\text{acceleration of block B}= \frac{g}{7}$.

Can somebody please tell me what's my mistake without just giving out the whole complete solution?

Thank you.

 

[Doc Al]

I could see that the block B has gravity acting on it, therefore the gravitational force on the block $B$ is $F_B = 5 g$ and hence the acceleration is $g$.

The string also exerts an upward force on block B (effectively), so its acceleration is not simply g. (It would be in free fall if it were.)

Set up force equations for each block.

 

[haruspex]

Further to @Doc Al's point, this is also wrong:

therefore tension on each string will be half of $F_B$

If that were the tension in the string then mass B would not fall.

 

[Adesh]

Okay, let the tensions in the strings connected to the pulley of block B be $T_1$ on each string. So, net force on block $B$ is $F_{net}= 5g - 2T_1$. And therefore, the force on block A is $F= T_1$.

 

[Frigus]

Homework Statement:: Find the acceleration of block A and block B.
Relevant Equations:: $F=ma$.

the correct answers are acceleration of block A=27g and acceleration of block B=g7.

Please check again that correct answers are not 2/7g(downward) and g/7(upwards) but 10/13g(forward) and 5/13g(downwards).

 

[Frigus]

Okay, let the tensions in the strings connected to the pulley of block B be $T_1$ on each string. So, net force on block $B$ is $F_{net}= 5g - 2T_1$. And therefore, the force on block A is $F= T_1$.

Now you can use constraint motion equations to find relation between block a and b acceleration.

 

[Adesh]

Please check again that correct answers are not 2/7g(downward) and g/7(upwards) but 10/13g(forward) and 5/13g(downwards).

Oh sorry.

 

[Frigus]

Oh sorry.

No problem.

 

[Adesh]

@haruspex What should I do after post #4?

 

[haruspex]

@haruspex What should I do after post #4?

Write the ΣF=ma equation for each mass, and the kinematic equation relating the two accelerations.

 

[Adesh]

Write the ΣF=ma equation for each mass, and the kinematic equation relating the two accelerations.

For block B
$$
5g-2T_1= 5a_B $$
For block A
$$
T_1= 2a_A$$
Please explain me as I have no reason to believe that block A and B will have same acceleration.

 

[Frigus]

For block B
$$
5g-2T_1= 5a_B $$
For block A
$$
T_1= 2a_A$$
Please explain me as I have no reason to believe that block A and B will have same acceleration.

You are right...they don't have same acceleration.
Try to find relationship between their acceleration.
Study constraint motion equation ,they just require 10 minutes to understand and you will have new tool to solve pulley problems.

 

[haruspex]

For block B
$$
5g-2T_1= 5a_B $$
For block A
$$
T_1= 2a_A$$
Please explain me as I have no reason to believe that block A and B will have same acceleration.

Remember that the length of the string is constant. Write that as an equation relating the lengths of the different sections of string, and differentiate twice.

 

[Adesh]

Remember that the length of the string is constant. Write that as an equation relating the lengths of the different sections of string, and differentiate twice.

Let the length of the string from block A to the first pullet is $l_1$ and then from this pulley to the second pulley(to which block B is connected) is $l_2$. Length of string from block B to the pulley on right is $l_3$ and the last segment is $l_4$. What should I do next?

 

[haruspex]

Let the length of the string from block A to the first pullet is $l_1$ and then from this pulley to the second pulley(to which block B is connected) is $l_2$. Length of string from block B to the pulley on right is $l_3$ and the last segment is $l_4$. What should I do next?

Two of those are necessarily the same.
The sum is constant. What do you get if you differentiate that twice?

 

[Adesh]

Two of those are necessarily the same.
The sum is constant. What do you get if you differentiate that twice?

Yeah, I think $l_2 = l_3$. As the sum is constant, the first derivative (with time) will be zero, so will be the second derivative (with respect to time) . That is
$$
\frac{d^2}{dt^2} \left(l_1 +2 l_2+l_4\right) = 0 $$

 

[haruspex]

Yeah, I think $l_2 = l_3$. As the sum is constant, the first derivative (with time) will be zero, so will be the second derivative (with respect to time) . That is
$$
\frac{d^2}{dt^2} \left(l_1 +2 l_2+l_4\right) = 0 $$

Ok.
How do those derivatives relate to the accelerations of the blocks?

 

[Adesh]

Ok.
How do those derivatives relate to the accelerations of the blocks?

Okay, blocks should move as to maintain the length of strings, but I cannot do further than this. Can you provide a little more hint?

 

[Frigus]

Okay, blocks should move as to maintain the length of strings, but I cannot do further than this. Can you provide a little more hint?

 

[haruspex]

Okay, blocks should move as to maintain the length of strings, but I cannot do further than this. Can you provide a little more hint?

Expand
$$
\frac{d^2}{dt^2} \left(l_1 +2 l_2+l_4\right) $$
Evaluate the terms, using the variables for the accelerations of the blocks.

 

[Adesh]

Expand
$$
\frac{d^2}{dt^2} \left(l_1 +2 l_2+l_4\right) $$
Evaluate the terms, using the variables for the accelerations of the blocks.

$$\frac{d^2 l_1}{dt^2} + 2\frac{d^2 l_2}{dt^2} +\frac{d^2 l_4}{dt^2}=0 $$
$$
a_A +2 a_B =0 $$
$$a_A = -2 a_B$$
But sir, I really cannot convince myself why the second derivative of lengths are giving me the accelerations. Can you please help me in convincing myself?

 

[Doc Al]

But sir, I really cannot convince myself why the second derivative of lengths are giving me the accelerations. Can you please help me in convincing myself?

Express the position of each mass in terms of the lengths. (And correct your last equation.)

 

[Adesh]

Express the position of each mass in terms of the lengths. (And correct your last equation.)

Okay! We will take the pulley just after the block A as origin, and so we have position of block A as $(-l_1, 0)$ and position of block B is $(0, -l_2)$. Can you please tell me what’s the significance of constant length of string is here?

 

[haruspex]

Can you please tell me what’s the significance of constant length of string is here?

It gives you your equation in post #16.

 

[Adesh]

It gives you your equation in post #16.

Thank you everyone!

 

[haruspex]

we have position of block A as $(-l_1, 0)$

And what is the physical meaning of the second derivative of a position?

 

[Adesh]

And what is the physical meaning of the second derivative of a position?

Acceleration.

 

[haruspex]

Acceleration.

So what accelerations do the second derivatives of l₁ and l₂ represent?

 

[PhysicsBoi1908]

You could also get the constraint equations by putting the work done by string to zero, and then differentiating twice. This works here because the string is massless.

 

[Adesh]

So what accelerations do the second derivatives of l₁ and l₂ represent?

Accelerations of block A and block B.