- #1
greswd
- 764
- 20
To form a 2-torus, a narrow tube can be bent into a loop and joined end to end:
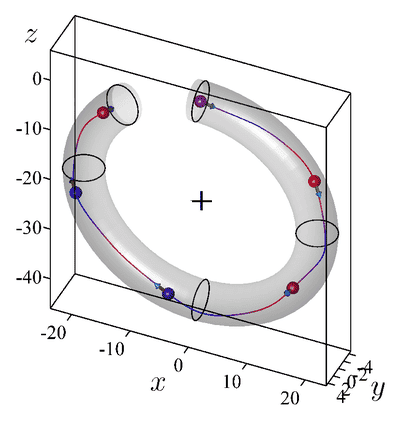
But instead of forming this loop in our three-dimensional space, the loop can also be formed in a direction perpendicular to three-dimensional space, moving it into the fourth dimension of space.
What's the name of this object?
Its similar to how the Klein bottle is a four-dimensional object, and this thing that we see is a poor three-dimensional representation

What's the name of this object?
Its similar to how the Klein bottle is a four-dimensional object, and this thing that we see is a poor three-dimensional representation