Wheel moving in rotation and translation

[JrK]

Hi :)

1/ First case

A wheel with a mass $m$ and a radius $r$ moves in horizontal translation and rotates around itself. The wheel is just above the ground, doesn't touch it. The wheel rotates CW if the wheel moves in translation to the right. The ground is horizontal and there is no gravity. The rotation of the wheel around itself is $\omega$ rd/s. The velocity of the translation of the wheel is $v=\omega*r$ m/s. The distance moved by the center of the wheel is exactly the distance moved by the rotation. From the ground, I apply a force $F_1$ on the wheel at the dot $A$, the force $F_1$ is horizontal, parallel to the ground. The ground receives the force $F_0$. For a small angle of rotation of the wheel, for example $1°$, I don't need near any energy to move the force $F_1$ because the distance of translation of the wheel is the distance moved by the rotation of the wheel around itself. For example, for 1° with a radius of $40$ mm, the distance moved by the center of the wheel is $0.7$ mm and the distance moved by the force $F_1$ is $0.000035$ mm. With the values: $F_1=F_4=F_0=F$. I win an energy of translation $F*v*t$ and I lost an energy from the rotation of the wheel $F*r*\omega*t$, so the sum of energy is well 0. I drew for a difference of angle of 10° but I studied only for 1°:

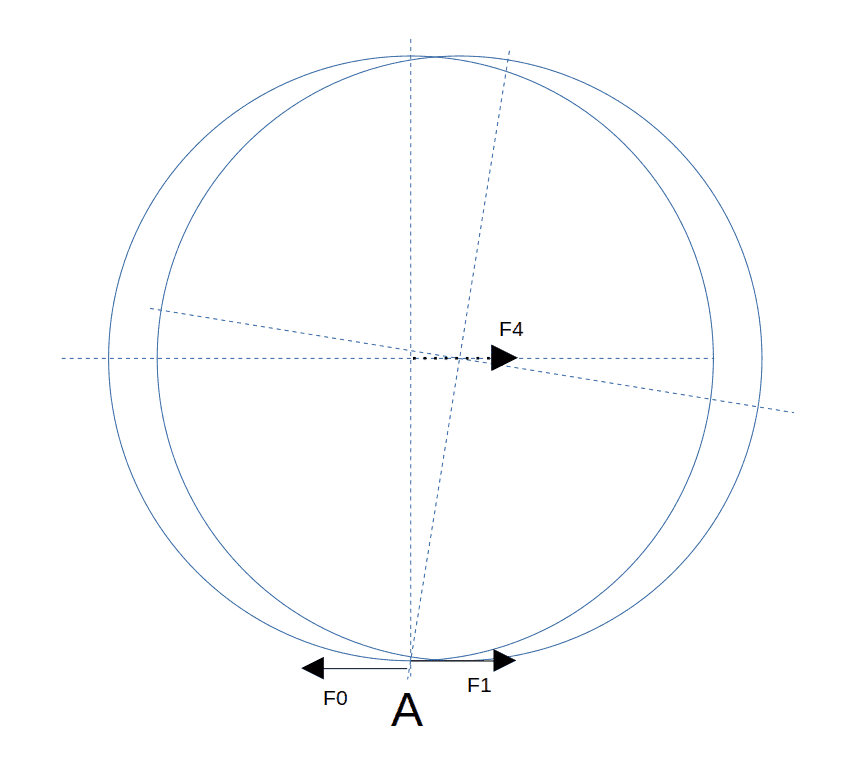
2/ Second case

I use now the device I explained in the thread: https://www.physicsforums.com/threa...on-compared-to-the-energy-of-rotation.990326/. Like I studied the sum of energy in that device, we know the distance moved by the center of the wheel is exactly the distance moved by the rotation around itself, it is like the wheel of the first case 1/. The gears can cancel the torque from the force $F_1$ with the force $F_2$, so there is no energy lost from the rotation: the gears prevent it. Like the sum of torques is 0, I can take a very low mass like I took in the device I studied before. The sum of forces on the center, on the horizontal axis (the vertical part of the sum of forces on the center cannot work because the wheel moves in horizontal translation), of the wheel is not $0$, it is $(1-\sqrt(2)/2)*F$, so the wheel wins an energy from the translation. The energy lost by the force $F_1$ in translation is very small compared to the energy wins by the center of the wheel, so I think the sum of forces on the center of the wheel is not like I think or the torque cannot be canceled by the gears. I drew the wheel at two positions, and a difference of 10°.

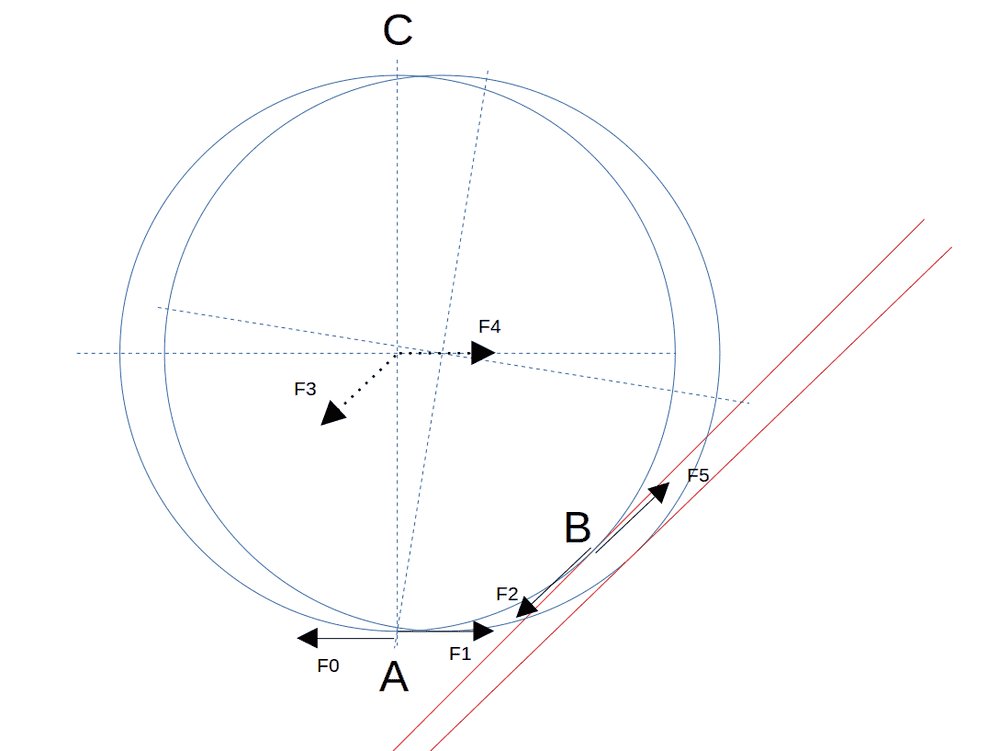
I apply the force $F_1$ on the dot $A$ to the wheel. The ground receives the force $F_0$. At the dot $B$, the gears cancel the torque from $A$, the gears applies the force $F_2$ to the wheel. The rack receives the force $F_5$. All the values of the forces from $F_0$ to $F_5$ is $F$. The sum of forces on the center of the wheel is $F_3+F_4$.

I can calculate the energy with equations, but for a small angle, I think it is not necessary because the difference of energy to move $F_1$ is very small compared to the energy wins by the center of the wheel in translation.

NB: In the device I studied with the gears before, I took the mass very small, with the wheel in the first case, I need a mass. But in the second case, like I cancel the torque from $F_1$ with the force from $F_2$, I don't need the mass, and the mass can be very low to forget it.

 

[BvU]

doesn't touch it

contradicts

From the ground, I apply a force $F_1$ on the wheel at the dot $A$

Anyway, if $\omega$ is constant and there is no friction, then there is no horizontal force either.

What is it you are trying to describe ?

 

[JrK]

contradicts

No, I can rotate the wheel around itself before and I can move the wheel in translation after. I don't use the ground to rotate the wheel.

Anyway, if is constant and there is no friction, then there is no horizontal force either.

Are you sure ? I apply the force F1 from the ground. I use the sum of energy to correct myself when I think alone, and in the first case I have well the sum of energy at 0, but ok, it is possible to make a double mistake.

What is it you are trying to describe ?

I think the torque on the second case is not like I described, but how to draw the forces on the center ?

 

[anorlunda]

The wheel is just above the ground, doesn't touch it.

From the ground, I apply a force F1 on the wheel at the dot A,

These contradict. If it doesn't touch, then no force is applied.

No, I can rotate the wheel around itself before and I can move the wheel in translation after. I don't use the ground to rotate the wheel.

That does not resolve the contradiction. Is the wheel touching or not?

 

[JrK]

Is the wheel touching or not?

No, I can translate the wheel just above the ground, at 1 µm (or less) above the ground. I don't want a direct interaction between the ground and the wheel. To have the force F1 on the wheel: I can apply the force from an electromagnet fixed on the ground for example in that case I can have a magnet fixed on the wheel. I can use a spring, even it is more difficult to test in reality, one end E1 of the spring is fixed on the ground, the other end E2 is blocked and when the wheel is at the good distance: I free the end E2 for a short time, after I re-block it.

 

[jbriggs444]

No, I can translate the wheel just above the ground, at 1 µm (or less) above the ground. I don't want a direct interaction between the ground and the wheel. To have the force F1 on the wheel: I can apply the force from an electromagnet fixed on the ground for example in that case I can have a magnet fixed on the wheel. I can use a spring, even it is more difficult to test in reality, one end E1 of the spring is fixed on the ground, the other end E2 is blocked and when the wheel is at the good distance: I free the end E2 for a short time, after I re-block it.

What effect are you trying to achieve with this? Do you want the wheel to be constrained to ride one micrometer above the surface of the Earth in a friction free manner?

So that there is no horizontal force between the two but there is a vertical force between the two?

If so, visualize the axle mounted on a friction free horizontal rail which is rigidly attached to the Earth. Now you can feel free to turn gravity back on. It won't matter.

 

[russ_watters]

You spent a ton of time earlier this month discussing similar poorly defined and convoluted examples and the discussions didn't seem to go anywhere useful. Can you tell us what you really want out of this so we don't waste our time chasing a point that doesn't seem to exist?

 

[JrK]

Do you want the wheel to be constrained to ride one micrometer above the surface of the Earth in a friction free manner?

Yes, the center of the wheel can be taken on a rail without any friction. The wheel rotates and moves in translation.

What effect are you trying to achieve with this?

I study the geometry of the circle and the line, I try to understand all the movements. Last time, I understood the movement of the wheel: the distance moved by the rotation is the same than the translation and that helped me to understand why I was wrong in the thread with the friction.

So that there is no horizontal force between the two but there is a vertical force between the two?

Not sure to understand, I apply an horizontal force from the ground to the wheel: F1. The rack applies the force F2.

Can you tell us what you really want out of this so we don't waste our time chasing a point that doesn't seem to exist?

I'm sorry if some people lost their time, I try to understand where are my mistakes, I help me with the sum of forces at 0, the sum of torques at 0 and the sum of energy at 0 but like it is cinematics it is not easy alone and when I don't find my mistake I ask. I hope AT could help me like he did before, he helped me a lot in others threads. If you think my questions are not worthy for that forum I will stop.

 

[jbriggs444]

Not sure to understand, I apply an horizontal force from the ground to the wheel: F1. The rack applies the force F2.

There is no force F2 on your drawing of the wheel rolling horizontally on the ground. There are F0, F1 and F4.

Please try to clarify one drawing at a time.

 

[JrK]

Please try to clarify one drawing at a time.

Ah, ok. The first case, I apply an horizontal force F1 to the wheel from the ground, the ground receives the force F0. The center of the wheel receives the force F4 (the axle) and the wheel will have a CCW torque on it.

 

[russ_watters]

I'm sorry if some people lost their time, I try to understand where are my mistakes, I help me with the sum of forces at 0, the sum of torques at 0 and the sum of energy at 0 but like it is cinematics it is not easy alone and when I don't find my mistake I ask. I hope AT could help me like he did before, he helped me a lot in others threads. If you think my questions are not worthy for that forum I will stop.

What I'd prefer is if you defined your problem better and consistently so it can be definitively solved. But I'm guessing that's a feature, not a bug...

Here's my perception, and it could be wrong: You are trying to design a device. You want the device to do *something*, which you won't say, and the physics is telling you the device won't work. So you add a new level of complexity, which includes an error that enables the device to work...at least until someone figures out and points out the error. Then you repeat the process. Indefinitely.

So what I'm really trying to ask is: is there a specific and self-contained purpose here or do you intend to keep changing the scenario indefinitely until it achieves a purpose you aren't going to tell us?

 

[jbriggs444]

We are still left wondering about the vertical force between ground and wheel. How is the wheel constrained to remain one micrometer from the surface of the Earth?

You say the center of the wheel "receives the force F4". By this, I guess that you mean that the axle is rigidly attached to the ground and that since the wheel is subject to horizontal force F1 from the ground and since it is constrained by the axle to rotate in place that it must be subject to an equal and opposite [unnamed] horizontal force from the axle. The third law partner to this is F4 whose horizontal component must be identical to F1.

No springs needed. Just an axle rigidly held in place.

If you are going to produce a free body diagram, please only show the forces that act on the free body.

 

[russ_watters]

Here's an example of what I'm referring to:

No, I can translate the wheel just above the ground, at 1 µm (or less) above the ground. I don't want a direct interaction between the ground and the wheel. To have the force F1 on the wheel: I can apply the force from an electromagnet fixed on the ground for example in that case I can have a magnet fixed on the wheel. I can use a spring, even it is more difficult to test in reality, one end E1 of the spring is fixed on the ground, the other end E2 is blocked and when the wheel is at the good distance: I free the end E2 for a short time, after I re-block it.

Electromagnet? Spring? Are they fixed in place? You've added a level of complexity that you're declining to fully define, but the details matter. You're trying to do an energy balance on a moving object, but a fixed spring or fixed electromagnet won't work to continuously apply a constant force to a moving wheel. This is probably a serious error, but it is too vaguely defined to be sure. Whatever you have in your head that this enables the device to do, but you won't tell us, is probably wrong because of this.

 

[JrK]

You've added a level of complexity that you're declining to fully define, but the details matter...to keep changing the scenario indefinitely

No, it is always the same example: a line and a circle, I changed the link in the previous thread and in this thread I added an external force for a short time: F1. I explained the first case to show I understood the sum of forces and the sum of energy but my problem comes from the second case. In the second case it is a wheel in rotation around itself and in translation, the link between the rack and the wheel: gears like I asked in the previous thread, and the external force F1 at the dot A during a short of time, I added in that thread. Even in the first case I added a mass, I don't need it in the second case.

but a fixed spring or fixed electromagnet won't work to continuously apply a constant force to a moving wheel.

Yes, I explained (after) with a spring and an electromagnet because I thought you need a real object. Use only an external force controlled in direction, value, time of application, etc. I counted the energy needed for that external force in the sum of the energy. Yes, it is better an external force.

Here's my perception, and it could be wrong: You are trying to design a device.

Not at all, I saw several mechanisms in a old serger machine (type of sewing machine) and I try to understand the links.

We are still left wondering about the vertical force between ground and wheel.

There is no gravity like I wrote in my first message. But if you want gravity, it is possible to have a rail to maintain the wheel above the ground (without any friction).

How is the wheel constrained to remain one micrometer from the surface of the Earth?

With a rail for example. The rail is fixed on the ground.

please only show the forces that act on the free body.

For the first case, I added the weight (if you need gravity) and the reaction of the rail on the wheel:

NB: for the first case, I don't have any problem, all is fine. It is for the second case where the sum of force in the center of the wheel seems to work.

Edit:

 

[jbriggs444]

So now we have a free body diagram where all the forces we care about have been removed. I'm out.

 

[Dale]

This whole thread is out. @JrK please simplify your scenario substantially and describe your simplified scenario fully before posting again.

The wheel is just above the ground, doesn't touch it.

From the ground, I apply a force

I don't use the ground to rotate the wheel.

I apply the force F1 from the ground.

To have the force F1 on the wheel: I can apply the force from an electromagnet

And make up your mind about the scenario beforehand and describe it simply, clearly, and without self contradiction.