Wheelie of a car coming out of a ditch: what is the correct model?

[alex33]

Homework Statement

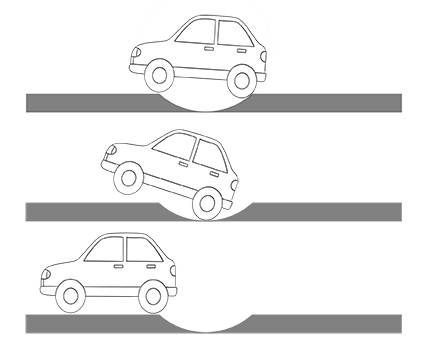
A 4x4 car is moving with constant speed V through a depression on the ground which can be approximate to an arc of a circumference, the length of which is equivalent to the wheelbase (inter axis) of the vehicle and the depth to half of the diameter of the wheels so that when the front wheels come out of the depression the rear ones are entering it. In that moment the vehicle rears up: the front wheels leave the ground, the rear ones continue their march inside the depression. After having drawn a short parabola in the air, the front wheels fall back to the ground, at the same time as the rear ones come out of the depression, detaching themselves from the ground only slightly. If possible, answer the following questions justifying the answer or why you cannot answers:

- Why do the front wheels leave the ground?
- Why are the rear wheels only slightly leave the ground?
- Is the weight of the vehicle equally distributed on the 4 wheels?
- Will the parabola drawn by the front wheels at the exit of the valley respond to the hourly law Z(x)=V0t+12Gt2 ? Are there other elements to take into account in the equation of motion? If possible, please write the correct equation.

Relevant Equations

Z(x)=V0t+1/2Gt^2

I ask for help in interpreting this question. Thank you !

 

[alex33]

I think the questions are very simple and direct, it's not an exercise where we have to do some calculations, perhaps this is a bit unusual, but here in Italy this is quite normal. Our math never adds up, but we're pretty deep in thought.

Why does the front of the machine lift off the ground? this is the first question. I would say there are more reasons. The first is that the velocity vector at the hole exit is inclined with respect to the ground due to the motion inside the crater itself. At the same time the rear of the car sinks into the hole.

Why do the rear wheels lift only slightly? The center of mass is probably shifted to the rear.

Can the trajectory be defined with an equation? For this I would need the help of some more competent and good-willed person. I think it is correct to apply the clockwise law of parabolic motion, but at the same time the center of mass is not on the front wheels, so something else must be written into the equation.

 

[haruspex]

Why does the front of the machine lift off the ground? this is the first question.

The text description of the geometry makes it clear that, for an instant, the car is level with each wheel right on the edge of the dip. In that case, it will not rear up. The rear wheels will lose contact with the ground briefly. The car will then start to rotate, but what is causing the rotation? The only force that can cause it is the normal force from the ground on the front wheels, so they do not leave the ground.
A bit later on, when the rear wheels hit the ground again, the front wheels might lose contact.

The next statement, "so that when the front wheels come out of the depression the rear ones are entering it", implies the width of the dip is a bit more than the wheelbase. The diagram shows that too. So the text description of the geometry must be wrong.

Correcting that,

the velocity vector at the hole exit is inclined with respect to the ground due to the motion inside the crater itself

Velocity vector of the car's mass centre? Isn't that on a downward path at this point? Why would that make the front wheels leave the ground?

Think about angular momentum.

 

[haruspex]

"hourly law Z(x)=V0t+12Gt2 ?"
Hourly law? Something lost in translation there.
Also, there is no x on the right hand side, so I guess you mean $Z(t)=V_0t+\frac 12gt^2$. (Note g, not G.)

clockwise law of parabolic motion

Again, there is no such law. Please clarify.

 

[alex33]

Dear haruspex
thanks for corrections...

... it's evident that the question is not written correctly since there are so many misunderstandings. This happens because I'm describing a real situation and I'm not writing an exercise. I start from a more complete illustration to try to explain myself better.

When the front wheels leave the dip, the rear ones have already entered: there is no a moment in which the car is horizontal over the hole, so the arc of the circle is a little longer than the wheelbase of the car. Not much more but enough.

Obviously the equation of motion I was referring to is:

$Z(t) = V_0t + \frac {1}{2}gt^2$

Is it written g and not G even if it is not the terrestrial g?

I'm going to start thinking about angular momentum...

Unfortunately the forum no longer allows me to change the initial question, so I ask all readers to start from this POST for any help. THANK YOU

 

[haruspex]

Dear haruspex
thanks for corrections...

... it's evident that the question is not written correctly since there are so many misunderstandings. This happens because I'm describing a real situation and I'm not writing an exercise. I start from a more complete illustration to try to explain myself better.

When the front wheels leave the dip, the rear ones have already entered: there is no a moment in which the car is horizontal over the hole, so the arc of the circle is a little longer than the wheelbase of the car. Not much more but enough.View attachment 326461
Obviously the equation of motion I was referring to is:

$Z(t) = V_0t + \frac {1}{2}gt^2$

Is it written g and not G even if it is not the terrestrial g?

I'm going to start thinking about angular momentum...

Unfortunately the forum no longer allows me to change the initial question, so I ask all readers to start from this POST for any help. THANK YOU

Ok. I should clarify something I wrote in post #2:

Velocity vector of the car's mass centre? Isn't that on a downward path at this point?

I am assuming there that the dip is only slightly longer than the wheelbase, and the mass centre of the car is somewhat behind the midpoint of the wheelbase, so is not yet over the midpoint of the dip.
The location of the mass centre may also be important for the second question.

 

[haruspex]

Doh! Please ignore most of my post #4. I'll start again.

Let's say the wheelbase exactly matches the dip. Just before the front wheels escape the dip, the rear is still on level ground, so the whole is rotating (clockwise in the diagram).
That won't instantly cease to be the case when the front climbs out if the dip, so the whole will be airborne. That makes it easy to model subsequent motion since there is no angular acceleration.

If the dip arc has radius r, the normals at the ends make angle $\theta$ to the vertical, and the rear wheels have horizontal speed v at this point, write equations for the trajectories of front and rear wheels while airborne.

 

[alex33]

Dear Haruspex
with this last clarification I already feel that we are closer to the solution...

The front wheels will follow the parabolic motion $Z(t) = V_0t + \frac {1}{2}gt^2$ ...right?
The rear ones will follow a uniform circular motion:
$θ(t) = θ_0 + ωt$ with $ω = \sqrt \frac {a_c}{r}$ up to the exit point of the dip.
But since the car is a unique body, shouldn't we write a single equation?

 

[haruspex]

Dear Haruspex
with this last clarification I already feel that we are closer to the solution...

The front wheels will follow the parabolic motion $Z(t) = V_0t + \frac {1}{2}gt^2$ ...right?
The rear ones will follow a uniform circular motion:
$θ(t) = θ_0 + ωt$ with $ω = \sqrt \frac {a_c}{r}$ up to the exit point of the dip.
But since the car is a unique body, shouldn't we write a single equation?

No, that's all wrong, I fear.
From the moment the rear wheels reach the dip and the front wheels exit it, the car is airborne. Its mass centre follows the usual parabola, but it is also rotating backwards at a constant rate. The wheels follow uniform circular motion relative to the mass centre, but it is not immediately clear whether the wheels are following parabolas relative to the ground.

To quantify that, we need to find expressions for velocity of the mass centre (horizontal and vertical components) and the rotation rate at the instant it becomes airborne.

 

[alex33]

it is also rotating backwards at a constant rate

...you mean the mass centre rotates clockwise?

I'm a bit confused... the wheels would have a uniform circular motion relative to the mass centere if the mass centre coincided with the centre of the dip arc, but it is clear that this is not the case since the dip is too shallow. We are rather in front of a motion on a semicircular guide ... am I wrong?

Do you think that if we moved from the theoretical problem to the real situation it would be clearer? I can post a slow motion video of the actual scene. I have all the information we need about the speed and center of gravity of the vehicle.

 

[jbriggs444]

...you mean the mass centre rotates clockwise?

The mass center is a point. Points cannot rotate. [Or, if they do, the rotation is unobservable and irrelevant]

I'm a bit confused... the wheels would have a uniform circular motion relative to the mass centere if the mass centre coincided with the centre of the dip arc, but it is clear that this is not the case since the dip is too shallow.

If both front and rear wheels are free from the ground, the car as a whole is in free fall, right?

If the car as a whole is in free fall, we may treat its motion as the ordinary translation of the center of mass with a rotation about the center of mass added to that.

There is no requirement that the car's mass center coincide with the center of the dip arc.

We are rather in front of a motion on a semicircular guide ... am I wrong?

I believe that we are describing the motion of the car after the front wheels have finished climbing out of the dip. They are unsupported, somewhere above the road. We are also describing the motion of the car after the rear wheels have moved forward clear of the lip of the dip. The rear wheels are also unsupported, somewhere above the dip.

The car is no longer being guided at all. It is in free fall at this point.

 

[alex33]

Dear jbriggs444 thanks for join this discussion !

The mass center is a point. Points cannot rotate.

Ok... sorry. I meant that the car rotates about its center of mass clockwise.

If both front and rear wheels are free from the ground, the car as a whole is in free fall, right?

This is not exact. When the front wheels lift off the ground the rear wheels continue to grip the ground and going down into the hole they still push the vehicle. This is what I see, if it can helps us I can post the slow motion movie, it will always be better than a simple drawing.

 

[jbriggs444]

This is not exact. When the front wheels lift off the ground the rear wheels continue to grip the ground and going down into the hole they still push the vehicle.

If the suspension is stiff and the wheel radius is small so that the curve of the tire is tighter then the curve of a free fall parabola then the rear tire should fly clear of the pavement rather than continuing to grip the ground as it drops into the dip.

If the suspension is loose, the motion of the rear tires will not accurately match the motion of the car during the period where the rear tires are beginning to drop into the dip.

This is what I see, if it can helps us I can post the slow motion movie, it will always be better than a simple drawing.

Real world cars have suspensions which allow wheel position to change relative to the car. This is a problem if we are have not decided on the level of detail of our models.

 

[alex33]

Dear jbriggs444
we are talking about the best model to interpret reality.

The wheels have a diameter of 82 cm (32 inch)
The travel speed of the vehicle at the exit of the dip is 2.38 m/s. The vehicle is well balanced on all 4 wheels (Centre of Gravity fairly central, slightly shifted towards the rear axis... by 20 cm over the total length of 3 metres).

The maximum height reached by the front wheels in the fall is about 30 cm (1 foot). In fact, the rear wheels could fall down at the entrance to the hole, rather than sticking to the ground, but it's not easy to verify. From what I see their size is greater than the curve of the free fall parabola. Also as you rightly said, this is a real vehicle that has suspension that adapts the wheels to the ground ...and quite well !

 

[jbriggs444]

we are talking about the best model to interpret reality.

"Best" can mean different things to different people. In this case, I take it that the model should incorporate the effect of springs, shock absorbers and tire radius, but perhaps not the flexibility of pneumatic tires or the angular momentum of the wheels. There is usually a trade-off between increasing the faithfulness of the model and keeping the model at a tolerable level of complexity.

If we are going to incorporate the effect of springs and shock absorbers, we need their characteristics included in the model.

Personally, I would be more comfortable starting with a simple model, verifying/validating its predictions and gradually adding complexity.

The wheels have a diameter of 82 cm (32 inch)

We might consider removing the wheels from the model by rounding off all the corners of the track, adding a 41 cm (16 inch) buffer. Then we could regard the wheels as pointlike supports following (or lifting free from) the modified track.

The travel speed of the vehicle at the exit of the dip is 2.38 m/s.

If we ignore the suspension for the moment, we can calculate whether the rear supports would come free from the pavement at the moment they cross the lip of the dip. That should be a fairly simple equation. The complications from rotation and translation should almost all cancel out at this moment.

 

[alex33]

I agree to simplify the model but I'm not sure if I understood what you are proposing... it would be like the car slipping on locked wheels, right? How could we understand whether the rear supports would come free from the pavement at the moment they cross the lip of the dip? by checking the rotation of the car around its centre of mass and at the same time its upward trajectory when it exits the dip?

Meanwhile I calculated that the rear wheels could not be in free fall in the dip, they would always touch the ground as the fall curve would be smaller than the curvature of the hole..

I have to be away for a few hours, but I'm starting to think about it...

 

[jbriggs444]

I agree to simplify the model but I'm not sure if I understood what you are proposing... it would be like the car slipping on locked wheels, right?

Yes. One might visualize tiny teflon skids.

How could we understand whether the rear supports would come free from the pavement at the moment they cross the lip of the dip? by checking the rotation of the car around its centre of mass and at the same time its upward trajectory when it exits the dip?

You would want to compare the normal component of the acceleration of the rear support point on a free falling and rotating car with the centripetal acceleration for a trajectory that remains in contact with the pavement.

Meanwhile I calculated that the rear wheels could not be in free fall in the dip, they would always touch the ground as the fall curve would be smaller than the curvature of the hole..

I'd not done the calculation... Mumble to myself... I get a different result.

 

[haruspex]

When the front wheels lift off the ground the rear wheels continue to grip the ground and going down into the hole they still push the vehicle.

Whether the suspension allows the wheels to remain in contact is not that relevant. The point of the suspension is to allow smooth movement of the chassis despite sudden dips and bumps. As the rear wheels fall into the dip, the compression force in the suspension is greatly reduced. Similarly at the front, as the front wheels escape the dip. The chassis is effectively in free fall.
That condition will last until the chassis motion brings the rear suspension back up to roughly its original compression. That will create a torque that arrests the rearing up at the front, so we do not need to analyse past that point to answer (a).

So ignore suspension; write the equations as I outlined in post #9, determine the angle of the chassis when the rear touches down, and let's see how that compares with observation of the peak angle.
If we conclude it is necessary to model the suspension, that will be too complicated for analysis. A simulation will be needed. However, that might not lead to a verbal explanation of how much it rears up, which I thought was the original purpose of the exercise.

 

[alex33]

Dear jbriggs444 and haruspex thanks again for your help.

I must insist that the rear wheels inside the dip remain in contact with the ground.

With an initial speed of 2.6 m/s if the car were in free fall when it descends into the dip it would reach the bottom of it in about 2/24 sec. At that moment, however, it would have traveled less than 15 cm on the X axis and this would not allow it to fall because the curvature of the dip is much lighter.

I confirm what haruspex says: my problem is finding the right model and identifying the correct equations, it's not doing the calculations. In this case, however, I will make use of a table to explain what happens to the rear wheels in the dip.

Centre of the arc AB (the dip arc): (X=0; Z=0)
Length of the arc: AB = 2,82 m
Radius of the arc: r = 2,972 m
Angle subtended by the arc AB: β = 2α = 40°
Angle between ground and arc tangent at A and B: α = 20°
Initial speed of the car at the entrance to the dip: V₀ = 2,6 m/s
g= 1,62 m/s²
X₀ = r*SEN(α)
Z₀ = r*COS(α)
Vx₀ = V₀*COS(α)
Vz₀ = V₀*SEN(α)
$Z(t)=Z_0 - Vz_0t+\frac {1}{2}gt^2$
$X(t)=X_0 - Vx_0t$
$X(z)=\sqrt {r^2-Z(t)^2}$ (retrieval of the X coordinate on the circumference arc, given Z)

t	Z(t)	X(t)	X(z)
0	-2,79101	1,02006	1,02006
0,042	-2,86972	0,85366	0,77134
0,083	-2,96546	0,77045	0,19055

I hope I have clarified the fact that the car is not in free fall.
Now I will reflect on your suggestions for finding the correct equations.
Here it is 4:30 am. I'll go to sleep first... See you tomorrow.

 

[Lnewqban]

... a depression on the ground which can be approximate to an arc of a circumference, the length of which is equivalent to the wheelbase (inter axis) of the vehicle and the depth to half of the diameter of the wheels so that when the front wheels come out of the depression the rear ones are entering it. In that moment the vehicle rears up: the front wheels leave the ground, the rear ones continue their march inside the depression.

The wheels have a diameter of 82 cm (32 inch)
The travel speed of the vehicle at the exit of the dip is 2.38 m/s. The vehicle is well balanced on all 4 wheels (Centre of Gravity fairly central, slightly shifted towards the rear axis... by 20 cm over the total length of 3 metres).

Centre of the arc AB (the dip arc): (X=0; Z=0)
Length of the arc: AB = 2,82 m
Radius of the arc: r = 2,972 m
Angle subtended by the arc AB: β = 2α = 40°
Angle between ground and arc tangent at A and B: α = 20°

If the distance between axles is 300 cm, as stated, all the numbers provided in this thread so far do not match.
I have tried a scale drawing following your descriptions.

 

[jbriggs444]

Dear jbriggs444 and haruspex thanks again for your help.

I must insist that the rear wheels inside the dip remain in contact with the ground.

With an initial speed of 2.6 m/s if the car were in free fall when it descends into the dip it would reach the bottom of it in about 2/24 sec. At that moment, however, it would have traveled less than 15 cm on the X axis and this would not allow it to fall because the curvature of the dip is much lighter.

I confirm what haruspex says: my problem is finding the right model and identifying the correct equations, it's not doing the calculations. In this case, however, I will make use of a table to explain what happens to the rear wheels in the dip.

Centre of the arc AB (the dip arc): (X=0; Z=0)
Length of the arc: AB = 2,82 m
Radius of the arc: r = 2,972 m

Wrong radius. We are talking about the convex lip of the dip, not the concave dip.

The axles would be traversing an arc with radius of 41 cm (0.41 meters) at a speed of 2.6 m/s as they come over the lip of the dip. The required acceleration is given by $\frac{v^2}{r} = 16.48$ m/s². That is greater than the downward acceleration of gravity. Barring suspension travel, the rear wheels will come free of the ground.

In addition, the axles are accelerated upward by the centripetal acceleration from the rotation of the car. But that just makes them lift further still.

 

[haruspex]

Length of the arc: AB = 2,82 m
Radius of the arc: r = 2,972 m
Angle subtended by the arc AB: β = 2α = 40°

That doesn't seem to add up. If by length of arc you mean the chord then that should be $2r\sin(\alpha)=2,02m$. If length along the arc, $2r\alpha=2,075m$.
I'll take the radius and angle as correct for now.

if the car were in free fall when it descends into the dip it would reach the bottom of it in about 2/24 sec

You are overlooking that the car's mass centre is rising when the rear wheels reach the dip.
Figuring out when the rear wheels touch down involves solving a quartic. I took the car's mass centre as being 0.5m above the ground normally, and ignored that the wheels have radius. Modelling it in a spreadsheet, I get that touchdown occurs after 0,46 seconds, with the rear wheels 0,3m past the midpoint of the dip. At that time, the car is tilted at 0,21 radians above the horizontal and the front wheels are 0,27m off the ground.

 

[alex33]

Good morning from Italy!

I am reading and evaluating your messages. I would like to anticipate you an error in the data published in the last post: a writing error... the Arc of circumference is 2.082 cm long NOT 2.82 cm (I means length along the arc 2rα)... I'm very sorry about this.

If the distance between axles is 300 cm, as stated, all the numbers provided in this thread so far do not match.

Dear Lnewqban distance between axles is 2,286 m (90 inch).
The overall length of the car is 310cm (122 inch)

I have tried a scale drawing following your descriptions.

...this will be very usefull THANKS !!!

The axles would be traversing an arc with radius of 41 cm (0.41 meters) at a speed of 2.6 m/s as they come over the lip of the dip.

I'm sorry... the radius is not 41 cm: this is the deep of the dip

You are overlooking that the car's mass centre is rising when the rear wheels reach the dip.
Figuring out when the rear wheels touch down involves solving a quartic. I took the car's mass centre as being 0.5m above the ground normally, and ignored that the wheels have radius. Modelling it in a spreadsheet, I get that touchdown occurs after 0,46 seconds, with the rear wheels 0,3m past the midpoint of the dip. At that time, the car is tilted at 0,21 radians above the horizontal and the front wheels are 0,27m off the ground.

Dear haruspex
what you have done is very interesting and the data you present is relatively confirmed by the pictures of the real event. Just consider that the vehicle's center of mass (which is a known measurement) is a bit lower: about 15 inches (38 cm) above the ground.
What would be more useful to know is when the front wheels would land on the ground, which is a verifiable fact.
I really can't solve a quartic... I'm good with spreadsheets, but can't you give me some help with equations? Thank you very much.

 

[haruspex]

the Arc of circumference is 2.082 cm long NOT 2.82 cm (I means length along the arc 2rα).

ok, but it made hardly any difference to the result I get.
(I assume you mean 2.082m, or as you would write it, 2,082m.)

 

[jbriggs444]

the radius is not 41 cm: this is the deep of the dip

Incorrect.

If the wheels were to remain in contact with the pavement as they pass over the lip of the dip, the axle would trace out a curve whose radius is equal to the tire radius. That is 41 cm.

 

[alex33]

If the wheels were to remain in contact with the pavement as they pass over the lip of the dip, they would trace out a curve whose radius is equal to the tire radius. That is 41 cm.

Dear jbriggs444 I don't know if we're talking about the same thing... I'll try to explain myself again with a drawing... sorry if it's not exactly in scale, but it should give you an idea: the radius of the wheel (0.41 m) is close to the depth of the hole (0.36 m) but it is only a small part of the radius of the dip (3 m).

 

[jbriggs444]

Dear jbriggs444 I don't know if we're talking about the same thing... I'll try to explain myself again with a drawing... sorry if it's not exactly in scale, but it should give you an idea: the radius of the wheel (0.41 m) is close to the depth of the hole (0.36 m) but it is only a small part of the radius of the dip (3 m).

View attachment 326544

Right. As I explained many times, I am talking about the rear wheels as they enter the dip. That is the interaction that is relevant to the behavior of the front wheels referenced in the problem statement.

 

[haruspex]

What would be more useful to know is when the front wheels would land on the ground,

That's a bit trickier. We have to make some assumption about how the rear wheels bounce and figure out the direction of bounce.

 

[alex33]

That's a bit trickier. We have to make some assumption about how the rear wheels bounce and figure out the direction of bounce.

OK! I agree with this. If it's complicated then it has to be done.

After we've done that, I'll post the video of the real event that sparked the need for this study. Did I mention this is not an exercise? Reality may be different from a model, but it has the advantage that it can be observed. From the images I have available I can say that:

1) the car does not change its trajectory on the y axis once it comes out from the hole
2) there doesn't seem to be an impact from the rear wheels inside the hole, the ride proceeds gradually without bouncing or violent impacts.

But let's start from the formulas of motion at the time the front wheels leave the ground and the rear wheels enter the hole, since you haven't answered me on these.

From your non-answer I understand that "I have to put my work into it" even if I don't have sufficient basis in physics, I venture in this... my first thought is that if it's true that we're in free fall (I still don't believe it , but I am willing to assume this hypothesis for the moment), from the centre of gravity to the front wheels the car has a parabolic upward motion, while from the centre of gravity to the rear wheels it has a parabolic downward motion. If I decompose the velocity vectors with respect to the centre of mass, I should find an equilibrium on Z axis provided that the centre of mass is exactly in the centre and the two motions actually start together. If they don't start exactly together the car chassis will maintain the inclination reached at the moment of equilibrium. The situation will change when the rear wheels get the bottom of the hole. That's not all but in the meantime is this right?

 

[haruspex]

the car does not change its trajectory on the y axis once it comes out from the hole

Sorry, not sure what you are saying there.

there doesn't seem to be an impact from the rear wheels inside the hole, the ride proceeds gradually without bouncing or violent impacts.

As I wrote, it's not whether the tyres actually leave the ground; it's whether the compression in the suspension is greatly reduced, making the chassis effectively in free fall. That said, I will continue to describe matters as where the wheels are, as though there is no suspension.

But let's start from the formulas of motion at the time the front wheels leave the ground and the rear wheels enter the hole, since you haven't answered me on these.

It is a homework forum, so I rather assumed you had high school background in ballistics. The equations of motion of a body in free fall are pretty simple. But the first step is to determine the velocity of the front wheels when free fall starts: horizontal and vertical components.
Can you do that, or do you want to say, hey, it's not homework, just give me the answers?

from the centre of gravity to the front wheels the car has a parabolic upward motion, while from the centre of gravity to the rear wheels it has a parabolic downward motion.

Not exactly.
The simplest way to look at it is that the centre of mass follows a parabola while the chassis rotates about it at a steady rate.

I have now added some spreadsheet lines for motion after the first touchdown. Again, please accept the rigid body view, i.e. it does bounce in effect.
I had to plug in a somewhat arbitrary value for the impulse from the ground. Just had to make it big enough that the rear does not continue down into the ground, but not so large that it increased the KE.
With a value at the low end of that range, I got that the rear touches down again just inside the dip, 0,3 seconds after the first touchdown. At this point, the front wheels were still 0,05 m off the ground.
With a value at the top end of that range, the front wheels hit the ground 0,3 seconds after the first touchdown, while the rear wheels were still 0,16m above ground.

 

[alex33]

Sorry, not sure what you are saying there.

I mean the car doesn't skid sideways (x-axis: horizontal, z-axis: vertical, y-axis: lateral)

As I wrote, it's not whether the tyres actually leave the ground; it's whether the compression in the suspension is greatly reduced, making the chassis effectively in free fall. That said, I will continue to describe matters as where the wheels are, as though there is no suspension.

OK !

It is a homework forum, so I rather assumed you had high school background in ballistics.

In fact I did a good scientific high school in Tuscany, the land of Leonardo da Vinci and Galileo. But that was from 1986 to 1991 !!!

Can you do that, or do you want to say, hey, it's not homework, just give me the answers?

Of course I'd rather get the right solutions myself, but you have to be very lenient with me, because my notions are very rusty. And keep in mind that I don't have to deliver any papers to any professors, or take any exams...

The simplest way to look at it is that the centre of mass follows a parabola while the chassis rotates about it at a steady rate.

May I ask what is the force (or what are the forces) that cause this second component of the motion?
As active forces in this scenario I can imagine the driving force of the vehicle, the weight force, the dynamic friction, the centripetal force. However, the latter ceases its action when the front wheels come out of the hole (to then act again on the rear wheels when they go up again).

Again, please accept the rigid body view, i.e. it does bounce in effect.

Ok... for the moment...

Just had to make it big enough that the rear does not continue down into the ground, but not so large that it increased the KE.

Of course total KE must be preserved

At this point, the front wheels were still 0,05 m off the ground.

Sorry, in doing the calculations did you use the right g that I posted? It's not the earthly one...

 

[haruspex]

May I ask what is the force (or what are the forces) that cause this second component of the motion?

Once it is in free fall, the only force is gravity. This means the horizontal velocity of the mass centre and the rotation about the mass centre are constant. The vertical velocity of the mass centre follows $v_y(t)=v_{y0}-gt$.

As active forces in this scenario I can imagine the driving force of the vehicle, the weight force, the dynamic friction, the centripetal force.

For a vehicle driving without skidding, the driving force is the frictional force. Without friction you'd get nowhere. Since we're discussing free fall here, neither applies.
Centripetal force is not an 'active' force. It is merely that component of the net force which is orthogonal to the velocity.

Of course total KE must be preserved

Not all. When it bounces (in your view, when the suspension goes through maximum compression) some is surely lost. But maybe not much in this case. Consider a horizontal uniform bar dropped so that one end strikes a fixed object. It is not hard to show that at most 1/4 of the KE is lost. The car landing in the dip is like that.
Indeed, if you don't see much bounce in the video then the loss must be close to the maximum.

you use the right g that I posted?

Yes.

 

[alex33]

Ok. I understand almost everything.

Once it is in free fall, the only force is gravity. This means the horizontal velocity of the mass centre and the rotation about the mass centre are constant.

With respect to rotation, you didn't answer explicitly... Do you mean that the rotation produced before the free fall by the circular guide of the dip is conserved around the centre of mass? Therefore it's different from a "uniform bar" which, when leaving the dip, follows a linear trajectory according to the tangent (as occurs in the sport of hammer throwing). Is that?

 

[alex33]

Ok. I understand almost everything.

With respect to rotation, you didn't answer explicitly... Do you mean that the rotation produced before the free fall by the circular guide of the dip is conserved around the centre of mass? Therefore it's different from a "uniform bar" which, when leaving the dip, follows a linear trajectory according to the tangent (as occurs in the sport of hammer throwing). Is that?

Oh no... it's the Angular Momentum !

 

[haruspex]

it's different from a "uniform bar" which, when leaving the dip, follows a linear trajectory according to the tangent (as occurs in the sport of hammer throwing).

Not sure if you are thinking of javelin, but in that case there's drag, which may cause some angular acceleration during flight. There is also the possibility that the thrower applied some downward rotation in the throw.

Oh no... it's the Angular Momentum !

Yes.