- #1
Haorong Wu
- 418
- 90
- TL;DR Summary
- When is the parallel axis theorem not appliable?
Hello, there. A friend asked me a problem last night.
Suppose that a system consists of a rod of length ##l## and mass ##m##, and a disk of radius ##R##. The mass of the disk is negligible. Now the system is rotating around an axis in the center of the disk and perpendicular to the plane where the rod and the disk lie in. What is the moment of inertia of the rod?
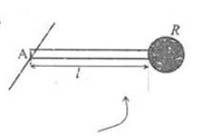
It is easy to have, by the definition,
##I=\int_R^{R+l} r^2 dm=\frac {m} {l}\int_R^{R+l} r^2 dr=\frac {m} {3l} [ \left (R+l \right ) ^3 -R^3 ]##.
Meanwhile, from the parallel axis theorem, I have
##I^{'}=\frac {ml^2} {12}+m (R+l/2)^2##.
Obviously, they do not match each other, since ##I## contains a term with ##R^3##, while ##I^{'}## does not.
I read the parallel axis theorem over and over again, but I could not see where I misunderstand.
Suppose that a system consists of a rod of length ##l## and mass ##m##, and a disk of radius ##R##. The mass of the disk is negligible. Now the system is rotating around an axis in the center of the disk and perpendicular to the plane where the rod and the disk lie in. What is the moment of inertia of the rod?
It is easy to have, by the definition,
##I=\int_R^{R+l} r^2 dm=\frac {m} {l}\int_R^{R+l} r^2 dr=\frac {m} {3l} [ \left (R+l \right ) ^3 -R^3 ]##.
Meanwhile, from the parallel axis theorem, I have
##I^{'}=\frac {ml^2} {12}+m (R+l/2)^2##.
Obviously, they do not match each other, since ##I## contains a term with ##R^3##, while ##I^{'}## does not.
I read the parallel axis theorem over and over again, but I could not see where I misunderstand.
Suppose a body of mass ##m## is rotated about an axis ##z## passing through the body's centre of mass. The body has a moment of inertia ##I_{cm}## with respect to this axis. The parallel axis theorem states that if the body is made to rotate instead about a new axis ##z^′ ## which is parallel to the first axis and displaced from it by a distance ##d##, then the moment of inertia ##I## with respect to the new axis is related to ##I_{cm}## by
##I=I_{cm}+md^2##.
Explicitly, ##d## is the perpendicular distance between the axes ##z## and ##z′##.
Last edited: