zenterix
- 774
- 84
- TL;DR Summary
- In a passage in the book Heat and Thermodynamics by Zemansky, the notation omits the variable for which limits are being taken. I would like to understand the limits better.
Here is a passage from a book I am reading
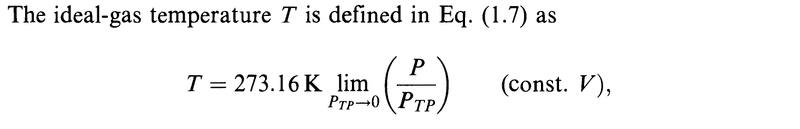

My question is about the limits.
Are all the limits in the derivation above done for ##P_{TP}\to 0##?
In particular, is it ##\lim\limits_{P_{TP}\to 0} (Pv)## that appears above?
The author omits this information in all but the first limit and it got me confused.
Here is a bit more context now to show why this has me confused.
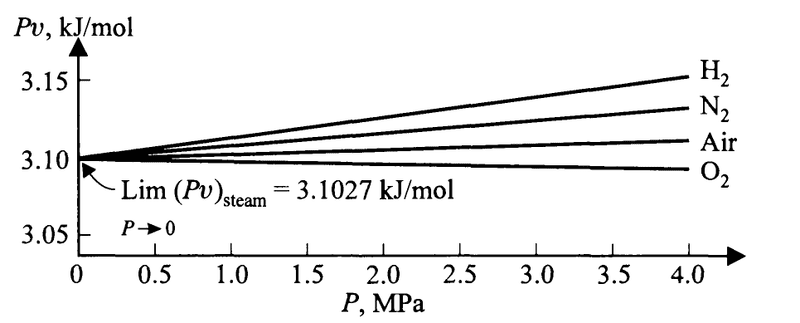
Just before the equations above, the book writes of the fact that if we plot ##Pv## against ##P## for different gases at a specific temperature, we see that for all of the gases the limiting value of ##Pv## as ##P\to 0## is the same.
Here is an example at the boiling point of water
Here is my attempt at explaining away the confusion
The ideal-gas temperature definition involves a limit in which we compute the value of ##P/P_{TP}## as ##P_{TP}## is made to approach zero at constant volume.
The way I understand this, a constant volume pressure thermometer is used. We have some particular temperature that we would like to measure, for example that of steam.
Now, in order to make ##P_{TP}## smaller, in each successive measurement we have the same volume of gas in the thermometer but we remove some gas from the thermometer: this way, the triple point of water is reached at a lower pressure for the same constant volume.
As we make these successive measurements, I think that the pressure ##P## associated with the steam will also be lower and will approach zero just like ##P_{TP}## (even though the ratio of these two pressures will approach a non-zero value).
Thus, it seems that ##\lim\limits_{P\to 0} (Pv)## is the same as ##\lim\limits_{P_{TP}\to 0} (Pv)##.
Is this what is happening?
My question is about the limits.
Are all the limits in the derivation above done for ##P_{TP}\to 0##?
In particular, is it ##\lim\limits_{P_{TP}\to 0} (Pv)## that appears above?
The author omits this information in all but the first limit and it got me confused.
Here is a bit more context now to show why this has me confused.
Just before the equations above, the book writes of the fact that if we plot ##Pv## against ##P## for different gases at a specific temperature, we see that for all of the gases the limiting value of ##Pv## as ##P\to 0## is the same.
Here is an example at the boiling point of water
Here is my attempt at explaining away the confusion
The ideal-gas temperature definition involves a limit in which we compute the value of ##P/P_{TP}## as ##P_{TP}## is made to approach zero at constant volume.
The way I understand this, a constant volume pressure thermometer is used. We have some particular temperature that we would like to measure, for example that of steam.
Now, in order to make ##P_{TP}## smaller, in each successive measurement we have the same volume of gas in the thermometer but we remove some gas from the thermometer: this way, the triple point of water is reached at a lower pressure for the same constant volume.
As we make these successive measurements, I think that the pressure ##P## associated with the steam will also be lower and will approach zero just like ##P_{TP}## (even though the ratio of these two pressures will approach a non-zero value).
Thus, it seems that ##\lim\limits_{P\to 0} (Pv)## is the same as ##\lim\limits_{P_{TP}\to 0} (Pv)##.
Is this what is happening?