Where are the one-sided derivatives of f(x) equal?

[karush]

$\tiny{s8.2.2.62} $
$f'(a)$ exists iff these one-sided derivatives exist and are equal.
(a) Find ${f'}_-(4)$ and ${f'}_+(4)$ for the function
$$f(x)=\begin{cases}
0 &if\quad x\le 0\\
5-x &if\quad 0<x<4\\
\dfrac{1}{5-x} &if\quad x\ge 4
\end{cases}$$
(b) Sketch the graph of $f$.

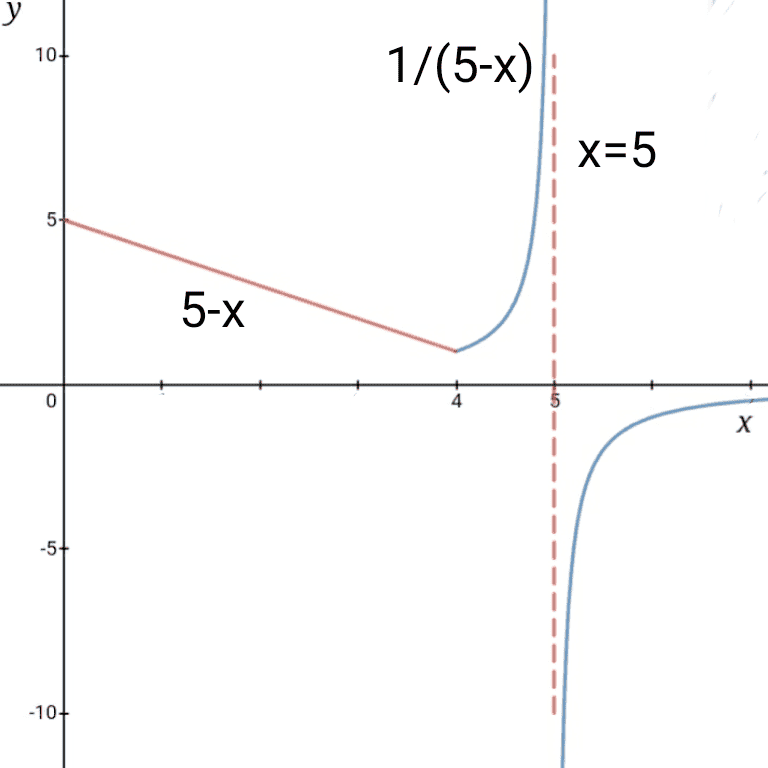
(c) Where is f discontinuous?
$x=5$
(d) Where is f not differentiable?
(4,1) cornerok where does the one sided derivative fit into this
c
also was going to try a tikx on this but have never done cases
this one was done in demos and modified in ibispaint took an hour

anyway typos, comments, etc

 

[Opalg]

ok where does the one sided derivative fit into this

It occurs at the point where $x=4$. The reason that there is a "corner" at that point is that the derivative on the left is $-1$ and the derivative on the right is $+1$.

 

[HOI]

Strictly speaking what you should do is calculate $\lim_{x\to 4^-}\frac{f(x)- 1}{x- 4}= \lim_{x\to 4}\frac{5- x- 1}{x- 4}= -1$ and $\lim_{x\to 4^+}\frac{f(x)- 1}{x- 4}= \lim_{x\to 4}\frac{\frac{1}{5- x}- 1}{x- 4}= \lim_{x\to 4}\frac{\frac{x- 4}{5- x}}{x- 4}= 1$ so, since those two "one-sided" limits are different, the derivative does not exist at x= 4.
Simpler, and probably what Opalg did, is to use the fact that, while a derivative is not necessarily continuous, it does satisfy the "intermediate value property", to argue:

For x between 0 and 4 f(x)=5-x so the derivative there is -1 and has limit, as x goes to 4, of -1. For x larger than 5, $f(x)= \frac{1}{5- x}= (5- x)^{-1}$ so the derivative there is $f'(x)=(-1)(5- x)^{2}(-1)= \frac{1}{(5- x)^2}$ and has limit, as x goes to 4, of 1. The two one-sided limits are not the same so the function is not differentiable at x= 4.