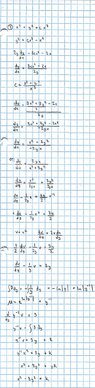Where Did I Go Wrong with Orthogonal Trajectories of x^2 + y^2 = cx^3?

[Pull and Twist]

Trying to figure out the orthogonal trajectory of x^2 + y^2=cx^3

Here's what I got... but it does not match the books answer. I don't know where I am going wrong. I think I was able to differentiate the equation correctly in order to get the inverted reciprocal slope and then I may have flubbed it trying to integrate. I ended up going from dy/dx to dx/dy so that I can get it in a format I can work with and used the Bernoulli method to integrate. Where did I go wrong?

View attachment 5504

 

[MarkFL]

We are given the family of curves:

$$x^2+y^2=cx^3$$

First, we want to express this family in the form $F(x,y)=k$:

$$x^{-1}+x^{-3}y^2=c\tag{1}$$

If can be shown that the orthogonal trajectories of (1) will satisfy:

$$\d{y}{x}=\frac{F_y}{F_x}=\frac{2x^{-3}y}{-x^{-2}-3x^{-4}y^2}=-\frac{2\dfrac{x}{y}}{\left(\dfrac{x}{y}\right)^2+3}$$

Now you have a first-order homogeneous ODE to solve...can you continue?

 

[Pull and Twist]

We are given the family of curves:

$$x^2+y^2=cx^3$$

First, we want to express this family in the form $F(x,y)=k$:

$$x^{-1}+x^{-3}y^2=c\tag{1}$$

If can be shown that the orthogonal trajectories of (1) will satisfy:

$$\d{y}{x}=\frac{F_y}{F_x}=\frac{2x^{-3}y}{-x^{-2}-3x^{-4}y^2}=-\frac{2\dfrac{x}{y}}{\left(\dfrac{x}{y}\right)^2+3}$$

Now you have a first-order homogeneous ODE to solve...can you continue?

Well I'll be ****ed... didn't even spot that... and all I had to do was multiply my OT equation by (1/y^2)/(1/y^2) to get it in that same format. I can definitely solve a first-order homogeneous ODE much more efficiently then the mess I was working with.