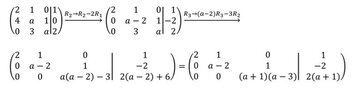Where is the Mistake? Solving a System of Equations

[Yankel]

Hello

I have a system of equations with the question "for which values of a the system has: a single solution, no solution and infinite number of solutions". In addition, I have some solution, and I need to find the mistake in the solution, I need some help with it...

So, for which values of a, the next system:

2x+y=1
4x+ay+z=0
3y+az=2

has a single solution, no solution and infinite number of solutions ?

View attachment 434

if a=2, the matrix has proportional rows (r2 and r3), and we get infinite number of solutions. However, if we set a=2 in the original system, there is a single solution.

Where is the mistake ?

Thanks !

 

[tkhunny]

You have it there in your graphic.

a = -1

This results in the third row disappearing, making an underfined system and infinitely many solutions.

a = 3

This results in an inappropriate result indicating no solution.

a = Anything Else

Unique Solution.

 

[Yankel]

yes, but put a=2, you get

2 1 0 1
0 0 1 -2
0 0 -3 6

now multiply the 3rd row by (1/3) and add the 2nd row to it, you get:

2 1 0 1
0 0 1 -2
0 0 0 0

which is not a single solution...something is wrong here...

 

[Opalg]

yes, but put a=2, you get

2 1 0 1
0 0 1 -2
0 0 -3 6

now multiply the 3rd row by (1/3) and add the 2nd row to it, you get:

2 1 0 1
0 0 1 -2
0 0 0 0

which is not a single solution...something is wrong here...

The operation $R_3 \to (a-2)R_3 -3R_2$ is the culprit. When $a=2$, that has the effect of killing the third row and replacing it by a multiple of the second row. So it is hardly surprising that rows 2 and 3 are then proportional. This is not so in the original system, it is something that you have introduced by performing a dodgy operation.

In fact, operations of the form $R_i\to pR_i+qR_j$ are best avoided unless $p=1.$ What you should have done instead of $R_3 \to (a-2)R_3 -3R_2$ is $R_2\to \frac1{a-2}R_2.$ When $a=2$ that gives a division by zero, which should have sounded an alarm bell and warned you to treat that case separately.

 

[Yankel]

Understood, thank you !