Where is the Point of Suspension to Keep a Suspended Rod Fixed?

[AbigailM]

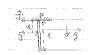
For prelim preparation. I've also included a figure of the problem.

Homework Statement

A stick of length l is suspended by one end at point P so that it hangs vertically and so that the top end of the stick does not move. A horizontal impulse J is applied perpendicular to the stick a distance a below the point of suspension. In general there will be an opposite impulse J' that must be given at the top of the stick (point P) to keep its point of suspension fixed. Find the distance a such that J'=0.

Homework Equations

$\tau=r\hspace{1 mm} x\hspace{1 mm} F$

$\tau=I\alpha$

L=T-U

The Attempt at a Solution

$L=\frac{1}{2}I\dot{\theta}^{2} +mg\frac{l}{2}cos\theta$

Using Lagrange's Equations
$I\alpha=-mg\frac{l}{2}sin\theta$

Equating the two equations for torque and setting r=a
$I\alpha = aFsin\theta$

Equate the last to equations
$aFsin\theta=-mg\frac{l}{2}sin\theta$

Solving for F
$F=-\frac{mgl}{2a}$

Therefore J is
$J=-\frac{mglt}{2a}$

So J' is
$J'=\frac{mglt}{2a}$

Is this looking correct? Gracias!

 

[crimsonidol]

I don't think that's right.

you have torque T=Fa since it applied perpendicular.
since it gives an impulse to balance the torque. if torque is zero no impulse. then a=0 is the point you are looking for i assume.

Your langrangian should have the constraint term too coming from the applied force.

 

[rude man]

You seemingly haven't solved for a, have you? a(J' = 0)?

I'm not up on Lagrangians any more but might look at the classical solution later.

OK, looked at it, seems simple if I did it right.

If you get an answer I'll tell you if it's what I got.

Hint: torques about the c.g. ?