- #1
russia123
- 5
- 0
I've looking at this and I'm dumbfound as to where to begin. Integrals have never been my strong suit.
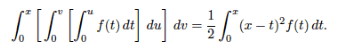
The process of proving an integral involves using mathematical techniques such as substitution, integration by parts, or trigonometric identities to manipulate the integral into a form that is easier to solve. It is important to understand the fundamental principles of integration and have a strong grasp of algebra before attempting to prove an integral.
The steps for proving an integral may vary depending on the specific integral being solved, but generally, the process involves identifying the appropriate method of integration, manipulating the integral to a solvable form, and then solving it using integration rules or techniques. It may also involve evaluating the integral at certain limits or using additional mathematical properties to simplify the solution.
While a calculator may be helpful in checking your work, it is not recommended to solely rely on a calculator to prove an integral. Understanding the concepts and techniques behind integration is crucial in solving integrals and relying too heavily on a calculator may hinder your understanding and ability to solve more complex integrals.
To check the correctness of your integral, you can differentiate the solution and see if it yields the original function. This is known as the fundamental theorem of calculus. Additionally, you can also check your solution using a calculator or by comparing it to known solutions or tables of integrals.
Some tips for proving integrals more efficiently include practicing frequently, understanding the properties and rules of integration, and being familiar with common techniques such as substitution and integration by parts. It is also helpful to break down the integral into smaller parts and to check your work along the way to avoid making mistakes.