alima
Gold Member
- 10
- 2
- Homework Statement
- Which is the probability of JohnCalls given Burglary? Why?
- Relevant Equations
- Bayes' Theorem = P (A|B) = ( P(B|A) * P(A) ) / P(B)
Questions:
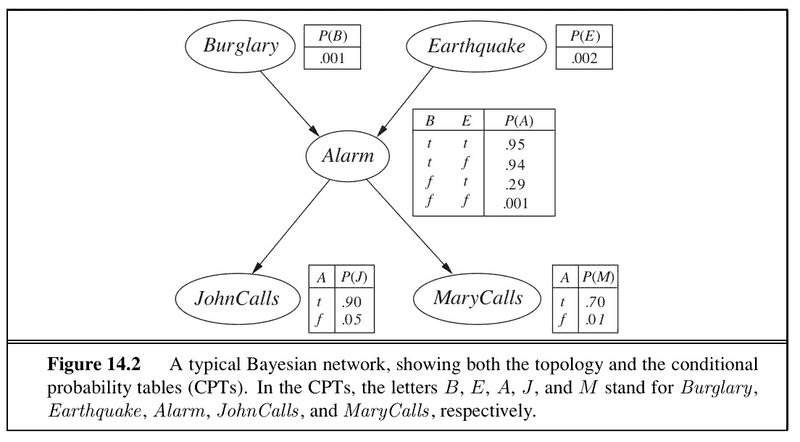
Source of the image: Artificial Intelligence: A Modern Approach - Third Edition, by Stuart Russell and Peter Norvig.
My attempt at solving: using Bayes' Theorem = P (A|B) = ( P(B|A) * P(A) ) / P(B)
P(JohnCalls|Burglary) = P(J|B) = ( P(B|J) * P(J) / P(B) )
- P (JohnCalls|Burglary) ?
- Why?
Source of the image: Artificial Intelligence: A Modern Approach - Third Edition, by Stuart Russell and Peter Norvig.
My attempt at solving: using Bayes' Theorem = P (A|B) = ( P(B|A) * P(A) ) / P(B)
P(JohnCalls|Burglary) = P(J|B) = ( P(B|J) * P(J) / P(B) )
- P(B): 0.001
- P(J): it depends on the Alarm ringing or not!
- P(B|J): how I am supposed to deduce this???