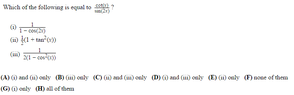- #1
Umar
- 37
- 0
Hello, sorry for the constant questions. But here is a question asking which of these are equal to the identity cot(x)/sin(2x).
I managed to find out that this is equal to the third option of the three, however, apparently this option on its own is not the right answer. I can't seem to get the other two options to be equivalent.
Can someone please help and see if there are other equivalencies?
View attachment 5965
I managed to find out that this is equal to the third option of the three, however, apparently this option on its own is not the right answer. I can't seem to get the other two options to be equivalent.
Can someone please help and see if there are other equivalencies?
View attachment 5965