- #1
jon4444
- 68
- 1
I ran across the explanation below of a car on a banked turn (no friction) on a High School teacher's website. I'm assuming this is incorrect, because how can the normal force in this situation equal mg/cos when an object on an inclined plane has a normal force equal to mg * cos? The high school teacher takes the normal force and breaks it into components and in the inclined plane we take the force of gravity and break it into components.
If someone could explain the discrepancy / fallacy here, I shall give them my first born:
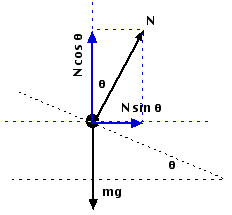 A free-body diagram for the car on the banked turn is shown at left. The banking angle between the road and the horizontal is
A free-body diagram for the car on the banked turn is shown at left. The banking angle between the road and the horizontal is
 (theta). The normal force, N, has been resolved into horizontal and vertical components (the blue vectors).
(theta). The normal force, N, has been resolved into horizontal and vertical components (the blue vectors).
In the vertical direction there is no acceleration, and:
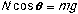
so:
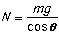
If someone could explain the discrepancy / fallacy here, I shall give them my first born:
In the vertical direction there is no acceleration, and:
so:
