jackiepollock
- 11
- 2
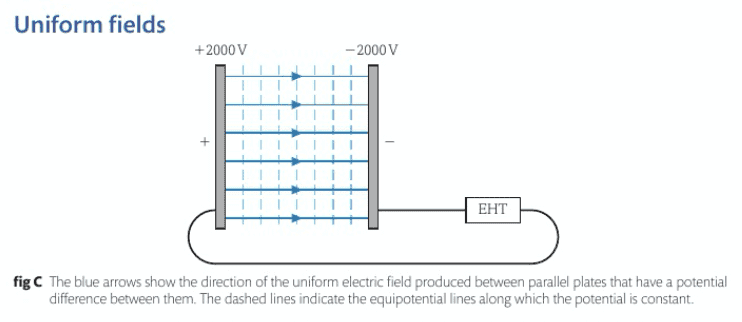
For a uniform field like this, I imagine the two plates that creates it are made of multiple atoms with charges, which are points sources that create radial fields. We know that radial fields don't have parallel fields lines, so how are parallel fields lines form when the field is made of various radial fields? Is it caused by the vector sums of these radial fields?