- #1
- 893
- 483
I'm reading about excitation of surface plasmons, and there's a claim in the derivation I don't know how to prove. The geometry is two infinite slabs of material with negligible permeability (##\mu_1 = \mu_2 = 1##) and different permittivity ##(\epsilon_1 \neq \epsilon_2 \neq 1)##. The claim is:
I know one could prove this by trial and error by just cranking out the boundary value problem with every possible combination of TE, TM and TEM modes, but I'm wondering if there is a more concise argument. (I'm preparing this content for a talk and want to be ready for this question with an answer that I can remember.)
I've attached an excerpt from the article:
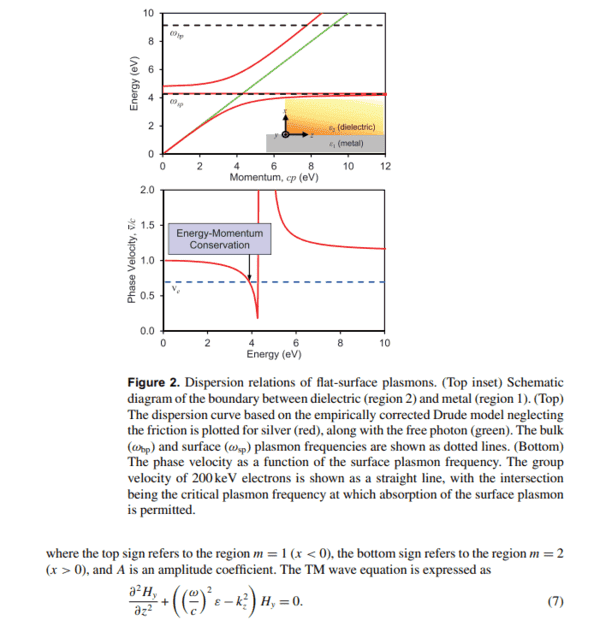My attempt:
The Gauss's law boundary condition for E-field implies that ##\epsilon_1 E_{1,x}|_S = \epsilon_2 E_{2,x}|_S##. In a TE wave, this transverse electric field ##E_x## generates an axial magnetic field ##H_z##. Because ##E_x## is not continuous across the interface, ##H_z## will not be continuous either. However, the Ampere's law boundary condition says that ##\hat{n} \times \vec{H_1}|_S = \hat{n} \times \vec{H_2}|_S##, which implies that ##H_{1,z}|_S = H_{2,z}|_S##. Gauss's and Ampere's laws cannot be satisfied simultaneously at the boundary for a TE wave, so TE modes are not allowed.
In a TEM wave, ##H_z = 0## but transverse E fields are allowed. It is obvious that ##E_x## must be 0 or you fall into the same conundrum as with TE waves with the boundary discontinuity (a non-zero ##E_x## would force ##H_z## to be discontinuous and therefore non-zero). However, I see no problem with having a TEM mode where the E-field is confined to the y axis. Have I made a mistake somewhere? My gut feeling is that TEM modes are only truly forbidden when the permeability is also discontinuous across the boundary, not just the permittivity.
I'm not feeling very confident in my attempt. Could anyone give this argument a sanity check?
Here's the source. The reference [25] that is cited for this statement about TM waves is: Maier S A 2007 Plasmonics: Fundamentals and Applications (New York: Springer), which I sadly don't have access to.
I know one could prove this by trial and error by just cranking out the boundary value problem with every possible combination of TE, TM and TEM modes, but I'm wondering if there is a more concise argument. (I'm preparing this content for a talk and want to be ready for this question with an answer that I can remember.)
I've attached an excerpt from the article:
The Gauss's law boundary condition for E-field implies that ##\epsilon_1 E_{1,x}|_S = \epsilon_2 E_{2,x}|_S##. In a TE wave, this transverse electric field ##E_x## generates an axial magnetic field ##H_z##. Because ##E_x## is not continuous across the interface, ##H_z## will not be continuous either. However, the Ampere's law boundary condition says that ##\hat{n} \times \vec{H_1}|_S = \hat{n} \times \vec{H_2}|_S##, which implies that ##H_{1,z}|_S = H_{2,z}|_S##. Gauss's and Ampere's laws cannot be satisfied simultaneously at the boundary for a TE wave, so TE modes are not allowed.
In a TEM wave, ##H_z = 0## but transverse E fields are allowed. It is obvious that ##E_x## must be 0 or you fall into the same conundrum as with TE waves with the boundary discontinuity (a non-zero ##E_x## would force ##H_z## to be discontinuous and therefore non-zero). However, I see no problem with having a TEM mode where the E-field is confined to the y axis. Have I made a mistake somewhere? My gut feeling is that TEM modes are only truly forbidden when the permeability is also discontinuous across the boundary, not just the permittivity.
I'm not feeling very confident in my attempt. Could anyone give this argument a sanity check?