Why are the values (-1.618, 0) and (0.618 ,0) solutions for this equation?

[pairofstrings]

TL;DR

I am trying to graph a plot for a simple equation but I am unable to perform the logic.

The equation is x² + x = 1; When I plot the values are (-1.618 , 0) and (0.618 , 0). Why are these numbers emerging from the equation? Can somebody help me with this?

Thanks in advance.

 

[anuttarasammyak]

Are you meaning plotting x y graph of
y=x^2+x-1?

 

[pairofstrings]

No. The following is the curve: $x^2 + x = 1$. I want to know why these values are emerging as (-1.618, 0) and (0.618 , 0)

 

[mcastillo356]

https://en.wikipedia.org/wiki/Algebraic_equation

Are you meaning plotting x y graph of
y=x^2+x-1?

Very interesting. No idea

 

[Ibix]

Because they're the solutions of the equation, perhaps...?

 

[jbriggs444]

Do you recognize the golden ratio there? The limiting ratio between successive terms of the Fibonacci sequence is the Golden ratio, 1.61803... to 1. The ratio is sometimes referred to as phi ($\phi$)

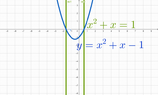
The polynomial that you are looking at, $x^2 + x - 1$ is the characteristic polynomial for a similar sequence given by $x_{n+2} = x_{n} - x_{n+1}$ which is basically the reverse of the Fibonacci sequence.

Obviously, if you start a Fibonnacci sequence with 0.61803... and 1, the next term will be 1.61803... You may have noticed that $1.61803... = \frac{1}{0.61803...}$. The ratio of consecutive terms in this particular sequence is always a constant equal to $\phi$.

As I recall, if you solve the Fibonacci recurrence you will get some linear combination $k_1 \phi^n + k_2 (-\phi)^{-n}$. For almost any first two terms you use, the limiting ratio of consecutive elements in the resulting sequence will be either $\phi$ or $-\phi$ in both directions.

If you are interested, we can walk through the details of recurrence relations and the methods for solving them.

You could also just use the quadratic formula, $\frac{-b \pm \sqrt{b^2-4ac}}{2a}$ on your polynomial: $x^2 + x - 1$ (a = 1, b = 1, c = -1) to get roots of $\frac{\sqrt{5}-1}{2}$ = $\frac{1}{\phi}$ = 0.61803... and $\frac{-\sqrt{5} - 1}{2}$ = $-\phi$ = -1.61803...

 

[anuttarasammyak]

Summary:: I am trying to graph a plot for a simple equation but I am unable to perform the logic.

The equation is x2 + x = 1; When I plot the values are (-1.618 , 0) and (0.618 , 0). Why are these numbers emerging from the equation? Can somebody help me with this?

I still do not understand what your ( , ) means but the values you refer seem to be solutions of the equation
x^2+x-1=0
namely
x=\frac{-1\pm\sqrt{5}}{2}

 

[Ibix]

I still do not understand what your ( , ) means

I'm pretty sure some packages use $(a,b)$ to mean $a+ib$. OP hasn't said what package produced this, which would be helpful to know.

 

[jbriggs444]

I am trying to graph a plot for a simple equation but I am unable to perform the logic.

Stepping back a bit. You were expecting a graph but instead got two points?

Probably should have written $y=x^2+x-1$ (an equation with two variables and a solution set that consists of a parabola on a plane) instead of $x^2 + x = 1$ (an equation with one variable and a solution set that consists of two points on a line).

 

[pairofstrings]

Because they're the solutions of the equation, perhaps...?

Thanks!

Probably should have written y=x2+x−1 (an equation with two variables and a solution set that consists of a parabola on a plane) instead of x2+x=1 (an equation with one variable and a solution set that consists of two two points on a line).

No, I need graph for $1 = x^2+x$.
How to know that if some random equation: $x^2 + x = 1$ has anything to do with Fibonacci series and Golden Ratio?
How do I know that (-1.618 , 0) and (0.618 , 0) are going to be solutions of the equation? The point is just moved 0.618 to left..

 

[phinds]

Because they're the solutions of the equation, perhaps...?

 

[phinds]

How do I know that (-1.618 , 0) and (0.618 , 0) are going to be solutions of the equation?

By solving the equation. Do you understand basic algebra? What grade are you in?

 

[pairofstrings]

By solving the equation. Do you understand basic algebra? What grade are you in?

Yes, I need to use formula for solving Quadratic Equation which is nice, and I don't need to try any other numbers because the formula will give me the exact values - roots.

 

[Ibix]

No, I need graph for $1 = x^2+x$.

This makes no sense to me. How did this arise? Is it a homework question? What exactly were you asked?

 

[phinds]

Yes, I need to use formula for solving Quadratic Equation which is nice, and I don't need to try any other numbers because the formula will give me the exact values - roots.

Then why did you even have a question in the first place?

 

[jbriggs444]

I need graph for $1 = x^2+x$.

The graph for that equation consists of two points: x=-1.61803 and x=0.61803.

There is no "y" in the equation, so there is no "y" in the graph.

 

[FactChecker]

Thanks!

No, I need graph for $1 = x^2+x$.

The graph of $1 = x^2+x$ is only two points, x=0.618 and x=-1.618 because those are the only two x-values that can satisfy the equation. There will not be a line in the graph, only two points.

 

[pairofstrings]

There are infinite numbers but I can find exactly that x = -1.618, y = 0 and x = 0.618, y = 0 as solutions to the equations by using the formula for Quadratic
equation? That means, I cannot use formula for Quadratic Equation to solve Cubic equation? Sorry, silly question.

 

[FactChecker]

Actually, the equation $1 = x^2 + x$ only says something about $x$. So $y$ can be anything. So the XY graph of the solution should be two vertical lines going through the X axis at the points $x = -1.618$ and $x = 0.618$.

 

[Ibix]

I'm guessing that this is homework that says something like "use a graphical method to solve $x^2+x=1$". Am I right, @pairofstrings?

 

[pairofstrings]

No.. there is another equation that goes like this: xy + x + y = 1, and I am trying to find a ubiquitous method to solve Qudratic, Cubic equation and many more. The equation itself explains little bit about graph: xy +x +y = 1; the equation says that there is a graph 'xy + x + y = 1' in which there is 'x = 1', 'y = 0' and there is 'y = 1', x = 0.
I can look into the graph and emerge with an equation and I can also look into equation and emerge with a graph, which can be witnessed in the equation: xy + x + y = 1
Here is the attachment for the explanation:

This reasoning is not working with $x^2 + x = 1$ as it gives me graph like this and the reasoning is not apt.

$x^2 + x = 1$
$x$ can't be 1. So, to satisfy the equation I am stuck with values of 'x' and 'y' as (-1.618 , 0) (0.618 , 0)?

 

[FactChecker]

No.. there is another equation that goes like this: xy + x + y = 1, and I am trying to find a ubiquitous method to solve Qudratic, Cubic equation and many more. The equation itself explains little bit about graph: xy +x +y = 1; the equation says that there is a graph 'xy + x + y = 1' in which there is 'x = 1', 'y = 0' and there is 'y = 1', x = 0.

Plus billions of other combinations. So what is the point?

I can look into the graph and emerge with an equation and I can also look into equation and emerge with a graph, which can be witnessed in the equation: xy + x + y = 1

What does this mean? It doesn't make sense to me.

 

[FactChecker]

There are a lot of additional techniques that you can apply when going between equations and their graphs. The intersection with the X and Y axis is not usually enough. In your $xy+x+y=1$ example, the two points that you mention are not enough since two points also define a straight line. At least you should also be looking for singular points and asymptotic behavior.

 

[pairofstrings]

In the equation: $xy + x + y = 1$, it is evident that $xy = 1$ is the curve to which I am adding $+x$ and $+y$ so the graph becomes like this:

I only get few values of $(x,y)$ from $xy + x+ y = 1$ when I equate $xy$ to one, $x$ to one and $y$ to one, but I at least know what the curve I am dealing with is and $+x$ and $+y$ are modifications to it. The points in the third quadrant are the points except one.

Here is $x y$ = 1

 

[jbriggs444]

the equation says that there is a graph 'xy = 1' in which there is 'x = 1', 'y = 0'

The pair x=1 and y=0 do not satisfy the equation xy=1.
The pair x=1 and y=0 do satisfy the equation xy + x + y = 1.

Edit: I note that the text quoted above has since been corrected to say that x=1, y=0 is a solution to 'xy + x + y = 1' rather than to 'xy = 1'.

 

[pairofstrings]

The pair x=1 and y=0 do not satisfy the equation xy=1.
The pair x=1 and y=0 do satisfy the equation xy + x + y = 1.

I am not saying that $y = 0$, in the equation $xy = 1$
I say that $x = 1$ and $y =1$ in the equation $xy = 1$, otherwise I will not get the graph of $xy = 1$ as shown in the attachment.

 

[Mark44]

There are infinite numbers but I can find exactly that x = -1.618, y = 0 and x = 0.618, y = 0 as solutions to the equations by using the formula for Quadratic
equation? That means, I cannot use formula for Quadratic Equation to solve Cubic equation?

The equation you started with, $x^2 + x = 1$ is a quadratic equation, so called because the highest degree of the variable is 2 (quadratum means "square" in Latin). You cannot use the quadratic formula to solve cubic (degree 3) or quartic (degree 4) equations, or other equations of higher degree.

Since y doesn't not appear in your equation, it is meaningless to include y = 0 in your solutions. The two solutions are merely two points on the real number line.

No.. there is another equation that goes like this: xy + x + y = 1, and I am trying to find a ubiquitous method to solve Qudratic, Cubic equation and many more. The equation itself explains little bit about graph: xy +x +y = 1; the equation says that there is a graph 'xy + x + y = 1' in which there is 'x = 1', 'y = 0' and there is 'y = 1', x = 0.

You asked exactly the same question some months ago. Since this new equation also includes y, the graph is two-dimensional. Yes, (1, 0) and (0, 1) are points on this graph, and there are infinitely many more points on this graph.

his reasoning is not working with x2+x=1 as it gives me graph like this and the reasoning is not apt.

Again, since y doesn't appear in this equation, the "graph" is just two points on the real number line.

In the equation: xy+x+y=1, it is evident that xy=1 is the curve to which I am adding +x and +y so the graph becomes like this:

Your analysis is faulty. It doesn't make sense to talk about adding x and y to an equation.

I only get few values of (x,y) from xy+x+y=1 when I equate xy to one, x to one and y to one

This also makes no sense. If xy = 1, and x = 1, and y = 1, then you have 1 + 1 + 1 = 1, which is clearly untrue.

 

[Mark44]

From post #3:

No. The following is the curve: x²+x=1.

This isn't a curve. The solution set consists of two points on the real number line.

 

[pairofstrings]

Okay. I thought it is an open curve. Anyways, never mind.

 

[jbriggs444]

Okay. I thought it is an open curve. Anyways, never mind.

The equation: $y=x^2 + x -1$ has a graph which is an open curve (a parabola opening upward) as was displayed some posts prior.

But $x^2 + x = 1$ and $y=x^2 + x -1$ are two different equations. They do not even have the same number of variables. Of course, their graphs will be different.

Taking a giant guess, you are (maybe) thinking about x,y graphs of the solution sets to algebraic equations involving two variables up to degree 2 and have hypothesized that these solutions are conic sections. But the graph for $x^2 + x - 1 = 0$ with y unconstrained does not appear to take such a form? But two parallel lines are a limiting case for a hyperbola.