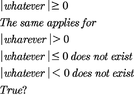- #1
mathdad
- 1,283
- 1
Explain why there are no real numbers that satisfy the equation
$$|x^2 + 4x| = - 12$$
How is this done algebraically?
$$|x^2 + 4x| = - 12$$
How is this done algebraically?
Last edited by a moderator: