Why can "dx" in integration be multiplied?

[Kelly333]

Hi,
This is an example in "Barron AP calculus"

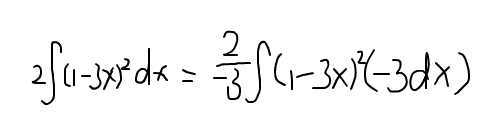
I learned from some past threads that "dx" in integration either means △x which is a infinite number or indicates the variable with respect to which you're integrating.
In the equation above, it seems that dx is multiplied by (1-3x)^2. Isn't dx just a notation?

I haven't learned definate integrals so far so please explain in detail if your answer is related to that.

Thanks.

 

[cnh1995]

△x which is a infinite number

I don't understand what you mean here by infinite number. It is an infinitesimally small change in x. If you refer definite integration expressed as a limit of sum, you'll see that dx is actually the infinitesimal width of the rectangular strip(area element) and y is the height of of the strip. Hence, it's area becomes y*dx and when you sum the areas of all such strips having width dx and height y over an interval, you get the total area under the curve. This sum is nothing but integration of y w.r.t x in that interval i.e.∫y⋅dx.

 

[HallsofIvy]

In this problem, "dx" is simply a symbol telling us which variable this is to be integrated with respect to. It never "means $\Delta x$ which is a infinite number"- I don't know where you got that! But it is not "multiplied by (1- 3x)^2". The notation here is just asking you to integrate the function $2(1- 3x)^2$ with respect to x.

 

[Kelly333]

In this problem, "dx" is simply a symbol telling us which variable this is to be integrated with respect to. It never "means $\Delta x$ which is a infinite number"- I don't know where you got that! But it is not "multiplied by (1- 3x)^2". The notation here is just asking you to integrate the function $2(1- 3x)^2$ with respect to x.

Thanks for your answer! If dx is just a symbol telling us which variable this is to be integrated with respect to, what does (-3*dx) actually means?

 

[Kelly333]

I don't understand what you mean here by infinite number. It is an infinitesimally small change in x. If you refer definite integration expressed as a limit of sum, you'll see that dx is actually the infinitesimal width of the rectangular strip(area element) and y is the height of of the strip. Hence, it's area becomes y*dx and when you sum the areas of all such strips having width dx and height y over an interval, you get the total area under the curve. This sum is nothing but integration of y w.r.t x in that interval i.e.∫y⋅dx.

Thanks for correcting that error! But in antidifferentiation, does dx also mean delta x?

 

[Ray Vickson]

Thanks for correcting that error! But in antidifferentiation, does dx also mean delta x?

No. Typically, we use the notation $\Delta x$ when writing finite sums such as $\sum_{i=1}^n f(x_i) \Delta x_i$, and $dx$ in the limit as we take $n \to \infty$ and each $\Delta x_i \to 0$. Of course, "$dx$" is just notation; it is not really "zero".

Now let's look in more detail at your little example. First, do you agree that initially we want to integrate $(1-3x)^2$ with respect to $x$? We can indicate this fact by introducing the $dx$ notation, but that is not really necessary. In some computer-algebra systems we drop the $dx$ altogether; for example, in Maple we can write "int((1-3*x)^2,x)" to indicate the integrand (before the ",") and the integration variable (after the ","). In Wolfram Alpha you can just enter "integrate (1-3*x)^2 with respect to x".

Anyway, we want to change variables to $y = 3x$, so the integrand involves the simpler-looking expression $(1-y^2)$. However, if we write $I_1 = \text{x-integral}\; (1-3x)^2$ and $I_2 = \text{y-integral}\; (1-y)^2$, we DO NOT have $I_1 = I_2$; in fact, we have $I_1 = \frac{1}{3} I_2$. Understanding this last equality is where the $dx, dy$ notation becomes helpful: if $y = 3 x$ then $dy = 3 dx$ and so $dx = \frac{1}{3} dy$. Now when we erase the $dx$ and $dy$ we are still left with the factor 1/3.

 

[Ssnow]

No, $\Delta x$ is not $d\,x$.

 

[Kelly333]

No. Typically, we use the notation $\Delta x$ when writing finite sums such as $\sum_{i=1}^n f(x_i) \Delta x_i$, and $dx$ in the limit as we take $n \to \infty$ and each $\Delta x_i \to 0$. Of course, "$dx$" is just notation; it is not really "zero".

Now let's look in more detail at your little example. First, do you agree that initially we want to integrate $(1-3x)^2$ with respect to $x$? We can indicate this fact by introducing the $dx$ notation, but that is not really necessary. In some computer-algebra systems we drop the $dx$ altogether; for example, in Maple we can write "int((1-3*x)^2,x)" to indicate the integrand (before the ",") and the integration variable (after the ","). In Wolfram Alpha you can just enter "integrate (1-3*x)^2 with respect to x".

Anyway, we want to change variables to $y = 3x$, so the integrand involves the simpler-looking expression $(1-y^2)$. However, if we write $I_1 = \text{x-integral}\; (1-3x)^2$ and $I_2 = \text{y-integral}\; (1-y)^2$, we DO NOT have $I_1 = I_2$; in fact, we have $I_1 = \frac{1}{3} I_2$. Understanding this last equality is where the $dx, dy$ notation becomes helpful: if $y = 3 x$ then $dy = 3 dx$ and so $dx = \frac{1}{3} dy$. Now when we erase the $dx$ and $dy$ we are still left with the factor 1/3.

Thanks!Your points are clear and easy to understand. Now I grasp the idea that dx is just a symbol but is also crucial in some equations.
But I don't believe it makes sense to multiply dx by (-3) in this equation in my example. Can you explain that?

 

[HallsofIvy]

Thanks for your answer! If dx is just a symbol telling us which variable this is to be integrated with respect to, what does (-3*dx) actually means?

By itself it doesn't mean anything! With an $\int$, $\int -3dx$ it would mean "integrate -3 x". Or, it could be a "differential". "dy= -3 dx" means that however x increases, y will decrease by three times that much. You should never see something like "f(x)dx" by itself. It should either be inside an integral, as $\int f(x) dx$, or in connection with some other differential, as $dy= f(x)dx$.

 

[Ray Vickson]

Thanks!Your points are clear and easy to understand. Now I grasp the idea that dx is just a symbol but is also crucial in some equations.
But I don't believe it makes sense to multiply dx by (-3) in this equation in my example. Can you explain that?

If you change variables to $y = 3x$ you get $\frac{1}{3} \int (1-y)^2 \; dy$, but if you change to $y = -3x$ you get $-\frac{1}{3} \int (1+y)^2 \, dy$.

You say " I don't believe it makes sense to multiply dx by (-3) in this equation in my example". Belief has nothing to do with it; there are standard change-of-variable formulas for integration, and they give you the 1/3 or -1/3 factor. What I mean is this: if we want to evaluate
$$I = \text{x-integral} \; f(x)$$
we may find it easier to change variables from $x$ to $y$, where $x = g(y)$, so that in the integral we will have $h(y) = f(g(y))$ instead of $f(x)$. However, that is not the end of the story: we also need to "transform the $dx$", giving
$$I = \text{y-integral} \; h(y) g'(y)$$
This is a provable theorem, not something subject to belief or dis-belief.