Why Can We Take Limits of Both Sides? [Answered]

[member 731016]

Homework Statement

Please see below

Relevant Equations

Please see below

For this,

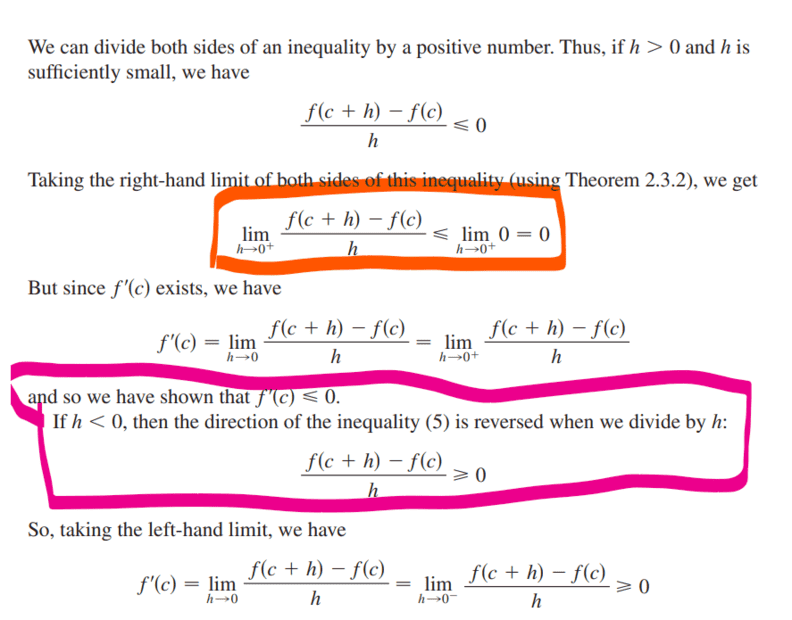
Does someone please know why we are allowed to take limits of both side [boxed in orange]?

Also for the thing boxed in pink, could we not divide by -h if $h > 0$?

Many thanks!

 

[Mark44]

Does someone please know

Yay!!!!

Does someone please know why we are allowed to take limits of both side [boxed in orange]?

If you have two expressions making up an equation or an inequality, you can take the limit of both sides. IOW, if two quantities are equal, their limits will be equal. Same holds for inequalities.

Also for the thing boxed in pink, could we not divide by -h if h>0?

The limit definition of the derivative (really, one such definition) has h in the denominator.

I'm guessing that there is some text that comes before what you have in the screen shot, something like $f(c + h) - f(c) \le 0$.
The goal is to get the left side in the form of the limit definition of the derivative, so they first divide both sides by h, which is assumed to be positive. Thus, the direction of the inequality doesn't change. After taking the limit, they conclude that $f'(c) \le 0$.

The rest of the work is to show that $f'(c) \ge 0$, with a final conclusion that f'(c) = 0.

 

[fresh_42]

It is indeed a bit tricky. For example if $3-h=2.999999999 = f(1-h) < 3$ as in one of your previous examples, we could and in the example would get $\lim_{h\to 0}f(1-h)=3.$ So all that can happen is, that the limit exists on the boundary: the function values are all smaller than three and the limit is equal to three. But this is all that could happen.

We have $\dfrac{f(c+h)-f(c)}{h}\leq 0.$ Imagine that $0$ be a wall and all points $\dfrac{f(c+h)-f(c)}{h}$ are on the left of this wall. You can get closer and closer to the wall, arbitrarily close by taking the limit, but you will always be left of it or at it; same as $2.99999999\ldots$ will always be smaller than $3,$ and in the limit equal to $3.$

If there would be a gap, say $\lim_{h\to 0} g(h)= C+1$ and $g(h)\leq C$ for all $h,$ then remember what a limit is. A limit has in every how ever small neighborhood always an element of the sequence that converges to this limit. Therefore, there must be some $h_0$ such that $|g(h_0)-(C+1)|< 1/3.$ Now, show that such a point $h_0$ cannot exist, if $g(h_0)<C.$

 

[FactChecker]

It's important that the step where limits are taken on both sides includes the '=' case, like:
if $g(x) \lt f(x)$, then $lim_{x \rightarrow a} g(x) \le lim_{x \rightarrow a} f(x)$.
The example you give does include the possibility that the limits are equal, so it is valid.