- #1
NODARman
- 57
- 13
- TL;DR Summary
- .
Can anyone explain to me why the second one is the right?
(See the attachment)
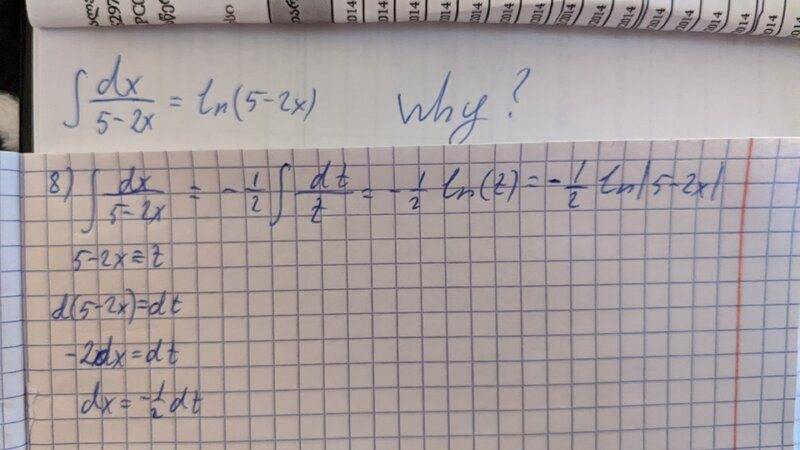
(See the attachment)
Why can't we just integrate a simple function?
In summary, integrating a simple function can be difficult due to the various types of functions and their unique properties. Some functions are easier to integrate due to known formulas or advanced techniques, while calculators and computers have limitations in accurately integrating all types of functions. Common challenges in integration include dealing with special behaviors and determining limits. Understanding integration is beneficial in many real-world applications, such as calculating areas and volumes in various fields of science and engineering.
- #2
- 27,241
- 18,653
The integral is the anti-derivative. What happens when you differentiate ##\ln(5 - 2x)##?
- #3
Office_Shredder
Staff Emeritus
Science Advisor
Gold Member
- 5,610
- 1,529
Your question is where does the ##-1/2## multiplier come from?
- #4
NODARman
- 57
- 13
Just got itPeroK said:
1. Why is it difficult to integrate a simple function?
Integrating a function involves finding the area under the curve of the function, which can be a complex process depending on the function. Even seemingly simple functions can have complicated derivatives, making integration challenging.
2. Can't a computer easily integrate a simple function?
While computers can perform mathematical calculations much faster than humans, they still require specific algorithms and methods to integrate a function. Some functions may require advanced techniques or approximations that cannot be easily programmed into a computer.
3. Is it possible to integrate any function?
There are some functions that cannot be integrated, or do not have a closed-form solution. These functions are known as non-integrable functions, and they often involve complex mathematical concepts such as infinite series or special functions.
4. Why do we need to integrate functions?
Integrating functions is an important tool in mathematics and physics, as it allows us to calculate areas, volumes, and other important quantities. It also helps us understand the behavior of a function and its relationship to other functions.
5. How can we make integration easier?
There are various techniques and methods for simplifying integration, such as substitution, integration by parts, and using tables of integrals. However, integration will always require a certain level of mathematical knowledge and understanding of the function being integrated.
Similar threads
-
Calculus
-
Calculus
-
Calculus