Why Do All Elements of a String Move Left in a Moving Reference Frame?

[Herricane]

I am trying to understand why v = (T/mu)^(1/2) Equation 16.18

EDIT: T is tension, mu is the mass divided by the length of the string, v is the speed of the wave on the string.

According to my book:

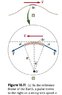
"Let us use a mechanical analysis to derive Equation 16.18. Consider a pulse mov-
ing on a taut string to the right with a uniform speed v measured relative to a sta-
tionary frame of reference as shown in Figure 16.11a (page 474). Instead of staying
in this reference frame, it is more convenient to choose a different inertial refer-
ence frame that moves along with the pulse with the same speed as the pulse so
that the pulse is at rest within the frame. This change of reference frame is permit-
ted because Newton’s laws are valid in either a stationary frame or one that moves
with constant velocity. In our new reference frame, shown in the magnified view
of Figure 16.11b, all elements of the string move to the left: a given element of the
string initially to the right of the pulse moves to the left, rises up and follows the
shape of the pulse, and then continues to move to the left. Both parts of Figure
16.11 show such an element at the instant it is located at the top of the pulse."

I don't understand why all elements of the string move to the left when the reference frame is moving at the same speed. I thought the motion would only be up and down.

 

[Spinnor]

Could you rephrase your question? The string elements move to the left (and a little up and down) because we are moving to the right as fast as the wave.

 

[Herricane]

Is the string or the pulse moving horizontally?

 

[Spinnor]

Is the string or the pulse moving horizontally?

There are two frames of reference in your derivation. In the first frame the pulse moves and string elements move only up and down. In the second frame you move with the velocity of the wave, the wave appears motionless but the string elements move to the left and up and down. So to answer your question the string "moves" in the second frame and the pulse moves in the first frame.

 

[asteriatic]

I can help clarify this concept for you. The equation v = (T/mu)^(1/2) represents the speed of a wave on a string, where T is the tension in the string and mu is the mass per unit length of the string. This equation is derived using a mechanical analysis, which involves considering the motion of a pulse on a taut string in two different reference frames.

In the first reference frame, the string is stationary and the pulse is moving to the right with a speed v. In the second reference frame, the entire frame is moving to the right with the same speed v as the pulse. This means that in the second reference frame, the pulse appears to be at rest.

Now, let's consider an element of the string that is initially located to the right of the pulse in the first reference frame. In the second reference frame, this element is also moving to the right with the same speed as the pulse. However, since the entire frame is moving to the right, this element will appear to be moving to the left relative to the frame. This is why all elements of the string appear to be moving to the left in the second reference frame.

This change of reference frame allows us to analyze the motion of the pulse more easily, as it is now at rest. Using this second reference frame, we can apply Newton's laws to derive the equation for the speed of the wave on the string.

I hope this helps clarify the concept for you. It is important to understand the concept of reference frames and how they can affect our analysis of physical phenomena. Keep exploring and asking questions, and you will continue to deepen your understanding of this and other scientific concepts.