jman115
- 2
- 0
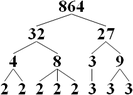
When I teach GCF to students, I show them how to find via the prime factorization and explain to them how the PF can get you all the factors of a number by multiplying different combinations of the Prime Factors and then proceed to explain why they are supposed to multiply the common Prime factors for the gcf.
My question is, why does multiplying different combinations of the prime factors get you ALL of the number's factors?
My question is, why does multiplying different combinations of the prime factors get you ALL of the number's factors?