Why Do I Get Negative Value Integrating y=-50e^-5x?

In summary: In the graph of the definite integral, we want the area bounded by the function y and the x and y-axis. However, when we take the integral, we are calculating the accumulated area, which may result in a negative value if the function dips below the x-axis. Therefore, the negative value in the definite integral is correct and corresponds to the area bounded by the function and the x-axis.
  • #1
bergausstein
191
0
Hello! And Good day!

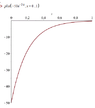
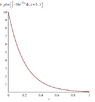
I just want to ask why do I keep getting a negative value whenever I take a definite integral of function $$y=-50e^{-5x}$$ the graph is shown as the first image.

If you look at the graph of the integral of "y" there's no traceable negative value on the graph. Why is that? Please help me understand why. Thanks!
 

Attachments

  • exponential.png
    exponential.png
    4.1 KB · Views: 92
  • exponential2.png
    exponential2.png
    4.8 KB · Views: 94
Physics news on Phys.org
  • #2
bergausstein said:
I just want to ask why do I keep getting a negative value whenever I take a definite integral of function $$y=-50e^{-5x}$$ the graph is shown as the first image.

If you look at the graph of the integral of "y" there's no traceable negative value on the graph. Why is that? Please help me understand why. Thanks!
The first plot correctly shows the graph of the function $-50e^{-5x}$, which is always negative as $x$ goes from $0$ to $1$.

The second plot does not make sense at all, if you are trying to find the area of the region between the graph and the axis. That is given by a definite integral, so it is just a number, not a graph. In fact, $$\int_0^1-50e^{-5x}dx = \bigl[10e^{-5x}\bigr]_0^1 = 10(e^{-5} - 1) \approx -9.9326.$$ That answer is negative, corresponding to the fact that the region lies below the $x$-axis.
 
  • #3
Opalg said:
The first plot correctly shows the graph of the function $-50e^{-5x}$, which is always negative as $x$ goes from $0$ to $1$.

The second plot does not make sense at all, if you are trying to find the area of the region between the graph and the axis. That is given by a definite integral, so it is just a number, not a graph. In fact, $$\int_0^1-50e^{-5x}dx = \bigl[10e^{-5x}\bigr]_0^1 = 10(e^{-5} - 1) \approx -9.9326.$$ That answer is negative, corresponding to the fact that the region lies below the $x$-axis.

Is it not that the area bounded by the function y and the x and y-axis corresponds to the y values of the integral of y? I''m still confused.
 
  • #4
http://mathhelpboards.com/attachments/calculus-10/6521d1491653833-area-calculation-exponential2-png
First, note $\displaystyle f(x) = \int -50e^{-5x} \, dx = 10e^{-5x} + C$ Your plot above assumes $C = 0$. Fact is, it should be shifted down 10 units since $C=-10$ for the following reason ...

Consider the definite integral as a function ... $\displaystyle f(x) = \int_0^x -50e^{-5t} \, dt \implies f(0) = 0$ The y-values of the definite integral "accumulation" function are indeed negative. Graph is attached. Also note the evaluation of $f(1)$ calculated previously by Opalg using the FTC ...

View attachment 6544
 
  • #5
The integral function is positive but decreasing. If b> a then f(b)< f(a) so that f(b)- f(a) is negative.
 

FAQ: Why Do I Get Negative Value Integrating y=-50e^-5x?

1. Why does the value of y become negative when integrating y=-50e^-5x?

The negative value of y when integrating y=-50e^-5x is due to the negative coefficient, -50, in front of the exponential function. When integrating, the negative sign is carried through the process and results in a negative value.

2. Can a negative value be obtained when integrating exponential functions?

Yes, it is possible to obtain a negative value when integrating exponential functions. This is especially true when there is a negative coefficient or when the limits of integration result in a negative area under the curve.

3. What does the negative value represent in the context of the function y=-50e^-5x?

In this context, the negative value represents a decrease in the original function. This is because the negative sign indicates that the function is decreasing as x increases. This can be seen graphically as a downward-sloping curve.

4. Is there a way to obtain a positive value when integrating y=-50e^-5x?

Yes, it is possible to obtain a positive value when integrating y=-50e^-5x. This can occur when the limits of integration result in a positive area under the curve, or when the negative coefficient is canceled out by a positive constant or coefficient in front of the function.

5. How can I avoid getting a negative value when integrating y=-50e^-5x?

To avoid getting a negative value when integrating y=-50e^-5x, you can change the limits of integration or manipulate the function to include a positive coefficient. You can also use absolute value or apply the appropriate rules of integration to ensure a positive result.

Similar threads

I Negative area above x-axis from integrating x^2?
Replies
4
Views
2K
B Calculating shaded area: I'm getting discrepancies between methods
Replies
3
Views
1K
I Double integrals - do areas cancel?
Replies
24
Views
3K
I How to evaluate the enclosed area of this implicit curve?
Replies
2
Views
2K
MHB How to Find the Surface Area of a Pringle Using Double Integration?
Replies
1
Views
2K
I Find the area enclosed by the curve y = x csch(x+y)
Replies
3
Views
1K
I The Basic Area Problem (introduction to the topic of integrals)
Replies
24
Views
3K
I Why is the integral of ##\arcsin(\sin(x))## so divisive?
Replies
3
Views
2K
I Area under curve using Excel question
Replies
2
Views
1K
I Question about Integrals to Determine Volume vs Surface Area
Replies
5
Views
957

Hot Threads

Recent Insights

Back
Top