Why Do Objects Fall Along Spacetime Ripples?

[Lars1408]

When people try to explain how gravity works, the following example is constantly used .

However, I don’t understand how this explains HOW gravity works. By using this example, gravity itself is used as a bias to explain how gravity works. How can explain gravity by saying “things fall along the curved space time”? You are using gravity to explain gravity. Its like saying “if you flip the switch the light goes on, that’s how electricity works”.

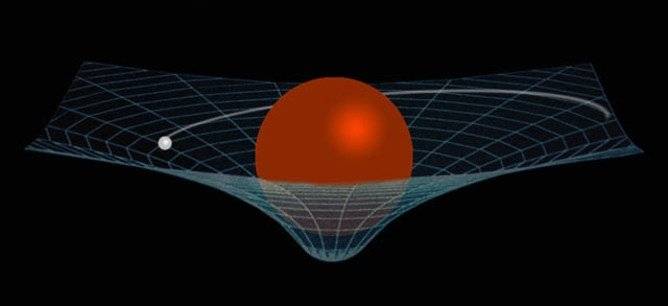
So why do things FALL along the fabric of space time? Why don’t they curve away from it? Why don’t they constantly move upwards and downwards the fabric like a wave? Why don’t they….?...

 

[PeroK]

Yes, it has nothing to do with rubber sheets, IMO. The short answer is that particles move according to the Lagrangian principle of least/greatest action. In this case, particles in curved spacetime follow paths that locally maximise the proper time the particle experiences. That's essentially the law of nature in GR that replaces Newton's first law.

 

[Ibix]

The rubber sheet model is of limited use. For a start, it implies that there's something outside spacetime into which objects could fall - there is no such thing as far as I am aware.

Spacetime is modeled as a curved manifold. Objects free fall along geodesics, which are the curved-spacetime generalisation of straight lines. The paths only look curved because we tend to look at 3d projections of the 4d geodesic. So the answer to "why do they follow curves" is the same as the answer to "why do things in flat spacetime move in straight lines". That's what they do. There are different ways of phrasing that, but there isn't really a deeper explanation at our current level of knowledge.

 

[phinds]

To put what has already been said in slightly different terms, they DON'T "fall", they follow geodesics. In Reimann Geometry, which is the geometry of spacetime (and gravity IS the geometry of spacetime), a geodesic is the equivalent of a straight line in Euclidean Geometry.

The "fall" you are getting is from the poor rubber-sheet analogy.

 

[Lars1408]

Yes, it has nothing to do with rubber sheets, IMO. The short answer is that particles move according to the Lagrangian principle of least/greatest action. In this case, particles in curved spacetime follow paths that locally maximise the proper time the particle experiences. That's essentially the law of nature in GR that replaces Newton's first law.

Could you please eleborate on this "particles in curved spacetime follow paths that locally maximise the proper time the particle experiences."? I don't fully understand what you mean by this.

 

[PeroK]

Could you please eleborate on this "particles in curved spacetime follow paths that locally maximise the proper time the particle experiences."? I don't fully understand what you mean by this.

Try this.

https://en.wikipedia.org/wiki/Geode...ty#Geodesics_as_curves_of_stationary_interval

 

[Lars1408]

The rubber sheet model is of limited use. For a start, it implies that there's something outside spacetime into which objects could fall - there is no such thing as far as I am aware.

Spacetime is modeled as a curved manifold. Objects free fall along geodesics, which are the curved-spacetime generalisation of straight lines. The paths only look curved because we tend to look at 3d projections of the 4d geodesic. So the answer to "why do they follow curves" is the same as the answer to "why do things in flat spacetime move in straight lines". That's what they do. There are different ways of phrasing that, but there isn't really a deeper explanation at our current level of knowledge.

So you can't look at the typical models literally? As if the spacetime fabric is being pulled downwards?

 

[Lars1408]

Try this.

https://en.wikipedia.org/wiki/Geode...ty#Geodesics_as_curves_of_stationary_interval

Thanks, I'll look into it.

 

[Nugatory]

So you can't look at the typical models literally? As if the spacetime fabric is being pulled downwards?

That’s right, you can’t. All that’s going on is that objects not subject to an external force are moving in a straight line at a constant speed just as Newton’s first two laws say they should... but doing so in a curved spacetime.

Imagine two people standing 10 meters apart at the equator. They both start walking in a straight line due North at a constant speed. Their paths are initially parallel, neither is moving even slightly sideways, but they will find themselves moving closer and closer to one another until they collide at the North Pole.

 

[PeroK]

Could you please eleborate on this "particles in curved spacetime follow paths that locally maximise the proper time the particle experiences."? I don't fully understand what you mean by this.

If we start with Newton's laws: they are originally formulated in terms of forces. But, thay can be reformulated using an approach developed by Lagrange. This can be shown to be entirely equivalent to Newton's laws, but instead of forces it uses the Lagrangian principle of least/greatest action. You can read up about this. It's also called the variational principle.

When it comes to GR there are no forces, so it's not possible to generalise Newton's laws to provide a law of motion for curved spacetime. But, it is possible to generalise the Lagrangian principle - and this is exactly what is done. If you consult a GR textbook you will find that the law of motion for a particle in curved spacetime is that it moves in such a way as to maximise its proper time.

Another way to say this is that particles follow the geodesics associated with a curved spacetime. And the geodescics are defined in terms of the Lagrangian principle and maximal proper time.

One interesting point is that in Classical (Newtonian) Mechanics a free particle (one with no forces on it) moves in a straight line, which is the shortest distance between two points.

In SR/GR a free particle moves along a path with the longest spacetime distance. For example, in the gravity-free flat spacetime of SR motion in a straight line at constant velocity (in an inertial reference frame) is actually the longest distance between two spacetime points, not the shortest.

 

[Ibix]

So you can't look at the typical models literally? As if the spacetime fabric is being pulled downwards?

No, you cannot take it literally. How would you define "down" without assuming the existence of some sort of gravitational force that causes the curvature that leads to gravity?

 

[Dale]

Could you please eleborate on this "particles in curved spacetime follow paths that locally maximise the proper time the particle experiences."? I don't fully understand what you mean by this.

This is about geometry. In Euclidean geometry the shortest distance between two points is a straight line. In other words a straight line is the path that locally minimizes the path length. Such a shortest-distance path is called a geodesic.

In physics we deal with spacetime instead of just space. Straight lines in spacetime are particularly important since by Newton’s 1st law that is the path of an inertial object (no external forces).

It turns out that the amount of time recorded on a clock (called proper time) is the spacetime length of the path, so a geodesic path is one that maximizes proper time. The sign is reversed (maximizing instead of minimizing) due to the way space and time are combined in spacetime.

So an inertially moving clock records the longest proper time between two points in spacetime for the same reason that a straight line is the shortest distance between two points. This is what the quote you cited means.

 

[A.T.]

So why do things FALL along the fabric of space time?

This might help:

 

[alantheastronomer]

Why does mass "curve" spacetime?...I don't know either!

 

[PAllen]

Why does mass "curve" spacetime?...I don't know either!

Well, given that the Einstein Field Equations put an equality between the Einstein tensor and the stress energy tensor, you could say that what is claimed is not that mass curves spacetime, but that curvature (specifically Ricci curvature) is matter, energy and pressure. Ultimately, of course, science doesn't focus on 'why' questions.

 

[Ibix]

you could say that what is claimed is not that mass curves spacetime, but that curvature (specifically Ricci curvature) is matter, energy and pressure.

But that still leaves Weyl curvature, the part of the curvature tensor that's also non-zero in vacuum, unexplained (a Whyl question? ...I'll get my coat). So at least part of the answer is "nobody knows". Yet.

 

[vanhees71]

I'd put it differently: The sources of the gravitational field is any from of energy, momentum, and stress of all other fields, which describe matter and radiation. The gravitational field itself can be reinterpreted as the curvature of pseudo-Riemannian spacetime with the pseudo-metric being the potentials of the gravitational field. I think it's good to have in mind both, the physical aspects of gravity as one of the fundamental interactions, and the aspect defining the geometry of spacetime.

It's of course a pretty complicated set of equations describing in principle simultaneously the geometry of spacetime and the dynamics of matter and radiation by a pretty complicated set of non-linear field equations. As some famous physicist (I think Wheeler) put it: The geometry of spacetime tells the matter how to move and the matter tells the spacetime how to curve (or something similar). The amazing thing is that in the geometric picture spactime is not just an unchangeable "container" of the dynamical entities as in Newtonian and special-relativistic physics but it is itself taking part in the dynamics.

Analogies like the rubber-sheet model are to be avoided, though at the first glance they seem to be intuitive, because they leads to wrong qualitative pictures, as already nicely discussed above.