Physicsperson123
- 5
- 0
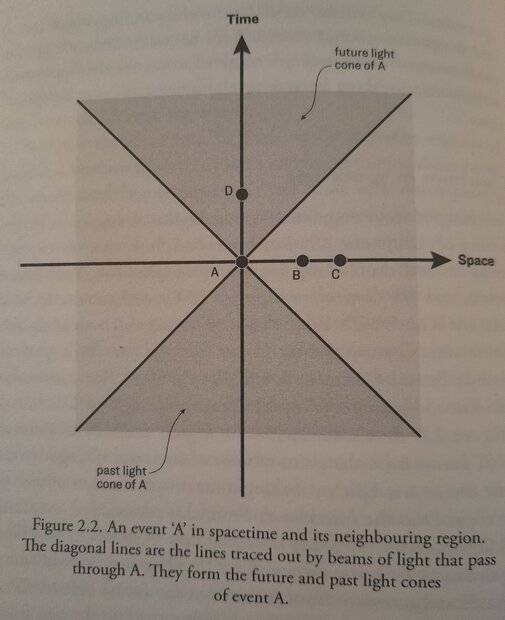
Here is the space-time diagram of an observer:
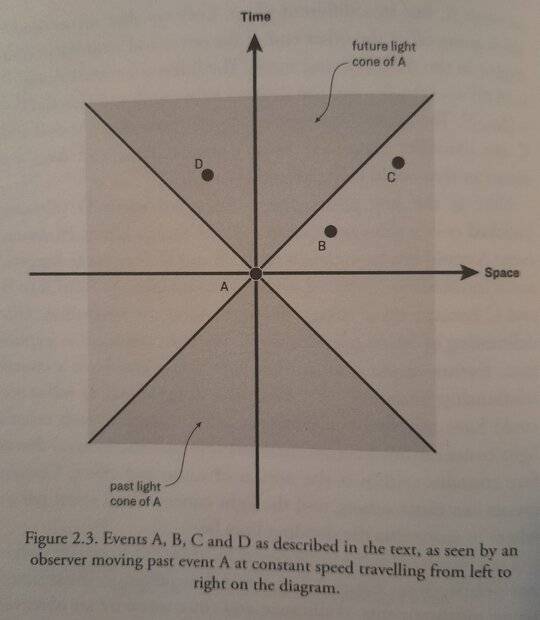
Here is the diagram as seen by an observer travelling from left to right:
I have attempted to represent the axis system of the moving observer on the axis system of the stationary observer in the following diagram:
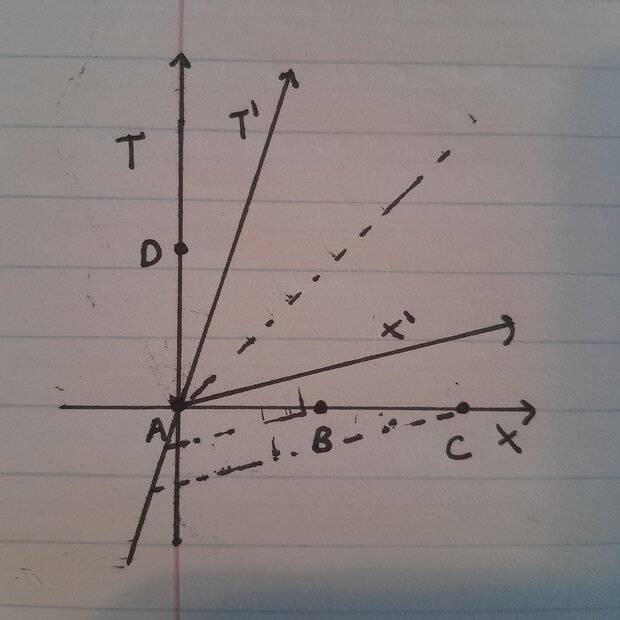
Event D seems to lie in accordance with the book diagram on the x' and y' axis. Events B and C, however, lie below the x'-axis, contrary to the book diagram.
What am I doing wrong, and what is the transformation shown in the book?
Help would be greatly appreciated!
Here is the diagram as seen by an observer travelling from left to right:
I have attempted to represent the axis system of the moving observer on the axis system of the stationary observer in the following diagram:
Event D seems to lie in accordance with the book diagram on the x' and y' axis. Events B and C, however, lie below the x'-axis, contrary to the book diagram.
What am I doing wrong, and what is the transformation shown in the book?
Help would be greatly appreciated!