Why Do the First Two Eigenvectors of a Periodic Potential Look the Way They Do?

[aaaa202]

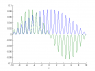
I am asked to simulate the first two eigenvectors for a periodic potential V(x)=V0cos(x). I have attached those two (blue is first, green is second). And I am then asked to explain why they look the way they do.
I wrote: Because a particle needs to tunnel through a lot of potential barriers to reach high and low x values it is natural that we see the wave function decreasing symmetrically about x=0. However I am not quite sure of this - does anyone think it sounds reasonable?

 

[Simon Bridge]

I think you need to characterize the functions: how do they look? What is striking about how they look?
Otherwise it just looks like you are hand-waving... specify what it is you are trying to explain.

i.e. it has a periodic part and an envelope part - what's special about them?

aside:
It looks like your potential is actually the sinusoid inside an infinite square well.

 

[aaaa202]

yes it is. But I don't think the fact that the potential is trapped inside a well dictates the behaviour at high lxl. Because I tried expanding the width of the well and then found that they went to zero way before the boundaries.
Well I don't really know what to say, other than the fact that they have a periodic part which is damped heavily as we move away from x=0. And then I tried to give an explanation for that using the idea of tunnelling.

 

[Simon Bridge]

I tried expanding the width of the well and then found that they went to zero way before the boundaries.

The envelope curve went to zero before the edges of the well? Wouldn't that only happen if the periodic function did not occupy the entire well? i.e. what is suppressing the envelope besides the infinite square well?

Anyway - guiding questions in post #2 still stand.

I'll add one:
What happens if you'd set periodic boundary conditions instead?

 

[paranormal]

Your explanation is on the right track, but let me elaborate further. An eigenfunction, in this case, refers to the wave function of a particle in a periodic potential. The periodic potential, V(x), in this case is described by the cosine function, which results in a series of potential barriers and wells with periodicity of 2π.

The first two eigenvectors, shown in blue and green, represent the lowest energy states of the particle in this potential. As you correctly mentioned, the wave function decreases symmetrically about x=0, indicating that the particle is most likely to be found near the potential wells and less likely to be found near the potential barriers. This is because the particle has a lower potential energy near the wells, making it easier for it to exist in those regions.

Furthermore, the shape and size of the eigenvectors also provide information about the energy levels of the particle. The blue eigenvector has a larger amplitude, indicating a higher probability of finding the particle in that region. This corresponds to a lower energy state, as the particle is more confined to the potential well. On the other hand, the green eigenvector has a smaller amplitude, indicating a higher energy state, as the particle is more likely to be found in the higher potential barrier regions.

In summary, the shape and behavior of the first two eigenvectors can be explained by the periodic nature of the potential and the energy levels of the particle. It is important to note that these eigenvectors are a result of the Schrödinger equation and are crucial in understanding the behavior of particles in quantum mechanics.