Why does a free particle in an infinite well have uncertainty bigger than h/2 ?

[drop_out_kid]

Homework Statement

verify the uncertainty principle by wave function of infinite well free particle(ground state)

Relevant Equations

\sai(x)=\sqrt {2/L} sin(Pi*x/L)dx

So I think I use the right approach and I get uncertainty like this:

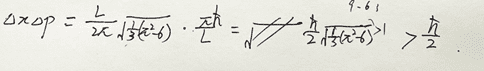
And it's interval irrelevant(ofc),

So what kind of wave function gives us \h_bar / 2 ? I guess a normal curve? if so, why is normal curve could be? if not then what's kind of wave function can reach the lower bound

 

[drop_out_kid]

Supplyment:
For <x^2>

for <x> it's simply L/2

for <p> it's simply 0

for <p^2> it's

by sin^2 integration.

 

[kuruman]

So what kind of wave function gives us \h_bar / 2 ? I guess a normal curve? if so, why is normal curve could be? if not then what's kind of wave function can reach the lower bound

Try the ground state for the harmonic oscillator of mass $m$ and frequency $\omega$.

 

[drop_out_kid]

Try the ground state for the harmonic oscillator of mass $m$ and frequency $\omega$.

Sorry I didn't get what that even is. We didn't learned that, I assume that's a ground state sinusoidal wave function?

 

[kuruman]

Sorry I didn't get what that even is. We didn't learned that, I assume that's a ground state sinusoidal wave function?

You asked and I replied. It is a Gaussian, $$\psi_0(x)=\left(\frac{m\omega}{\pi \hbar}\right)^{1/4}e^{-\frac{m \omega}{2\hbar}x^2}.$$Try it.