Why Does an Integrand Equaling Zero at x=1 Not Determine the Integral's Value?

[Hornbein]

I'm trying to calculate the volume of a truncated hypersphere. As part of it I want this integral.

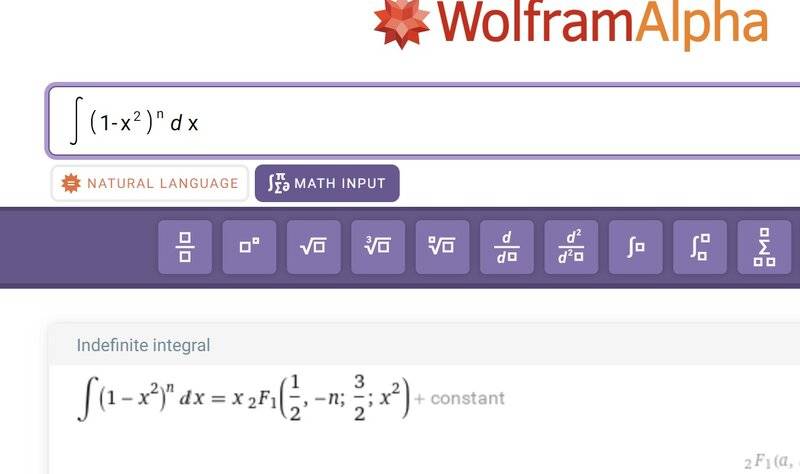
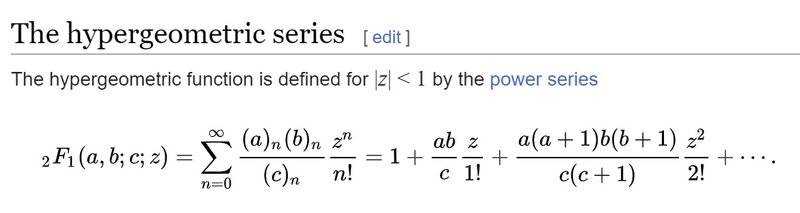
Clearly when x=1 the integrand is zero. But plugging this into the series give me a number greater than one. It is true that the series is not defined for x=1, but subtracting some tiny sum isn't going to make any difference.

I hope I'm missing something obvious.

 

[Bosko]

I made a mistake in my previous post ( deleted it ).

$$
\begin{align}
\int (1-x^2)^n ~dx &= \int (-x^2+1)^n ~dx \nonumber\\
&=\int \sum_{k=0}^n \binom {n}{k} (-x^2)^k1^{n-k}~dx \nonumber\\
&=\sum_{k=0}^n (-1)^k \binom {n}{k} \int x^{2k}~dx \nonumber\\
&=\sum_{k=0}^n (-1)^k \frac { n!}{k!(n-k)!} \cdot \frac {x^{2k+1}}{2k+1} \nonumber\\
\end{align}
$$

 

[pasmith]

Clearly when x=1 the integrand is zero. But plugging this into the series give me a number greater than one. It is true that the series is not defined for x=1, but subtracting some tiny sum isn't going to make any difference.

I hope I'm missing something obvious.

Why would the integrand being zero at $x = 1$ tell you anything about the value of the integral?