- #1
frzncactus
- 10
- 0
Problem 2.14: Explaining the Simplification from Street-Fighting Mathematics by Mahajan
"Why is the drag force independent of the gravitational acceleration g and of the cone's mass m (yet the force depends on the cone's shape and size)?"Context
Imagine two paper cones formed by taping together the edges of the cones shown in Figure 1 below. Both cones are similar in shape, but the larger cone has twice the height and width of the smaller cone. The cones are dropped point downward in the air. Mahajan proposes to "deduce the drag force as a function of fall speed and then to find the speed at which the drag balances the weight of the cones", thereby eliminating gravitational acceleration and cone mass.
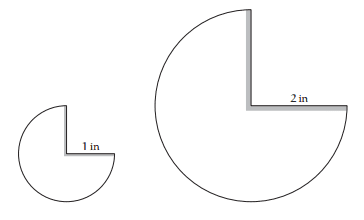
Figure 1. [itex]\frac{3}{2}\pi[/itex] sectors with radii 1" and 2", respectively
As an undergrad engineering student, I am familiar with seeing and applying the drag force equation
[itex]F_d=\frac{1}{2}\rho u^2 C_D A[/itex], but don't understand the physical basis for each of the terms present (and not present) in the formula. I would imagine that the drag force on a cone would be greater if a cone were dropped in an area of higher gravitational force (say, on Jupiter in a box filled with air similar in density to that on Earth). I could imagine that the velocity term is a function of something gravity-related, but don't fully understand why drag is independent of gravitational acceleration and mass. Please help me understand.
Attempt at a Solution 1
Revisiting some equations I remember deriving in general physics,
[itex]a=const=g[/itex]
integrating with respect to time, [itex]v=gt+v_0[/itex]
Those equations don't take friction into account, so I'm not sure how useful they are. At terminal velocity, velocity is constant and stops changing with respect to time. In that sense, i can see how g is no longer in the equation, but I would like to get a physical understanding of why this is true.
Attempt at a Solution 2
At terminal velocity, the net force on the falling object is zero. The only forces on the system are gravitational force ([itex]F_g=mg[/itex]) and drag force. They must be equal and opposite in magnitude for the sum of net forces to be zero, but that would mean that drag is a function of both mass and gravitational acceleration. This is why I am confused.
*Note: this is "pleasure reading", not a school assignment. I've been stuck on this page for a week and would be grateful for help!
"Why is the drag force independent of the gravitational acceleration g and of the cone's mass m (yet the force depends on the cone's shape and size)?"Context
Imagine two paper cones formed by taping together the edges of the cones shown in Figure 1 below. Both cones are similar in shape, but the larger cone has twice the height and width of the smaller cone. The cones are dropped point downward in the air. Mahajan proposes to "deduce the drag force as a function of fall speed and then to find the speed at which the drag balances the weight of the cones", thereby eliminating gravitational acceleration and cone mass.
Figure 1. [itex]\frac{3}{2}\pi[/itex] sectors with radii 1" and 2", respectively
As an undergrad engineering student, I am familiar with seeing and applying the drag force equation
[itex]F_d=\frac{1}{2}\rho u^2 C_D A[/itex], but don't understand the physical basis for each of the terms present (and not present) in the formula. I would imagine that the drag force on a cone would be greater if a cone were dropped in an area of higher gravitational force (say, on Jupiter in a box filled with air similar in density to that on Earth). I could imagine that the velocity term is a function of something gravity-related, but don't fully understand why drag is independent of gravitational acceleration and mass. Please help me understand.
Attempt at a Solution 1
Revisiting some equations I remember deriving in general physics,
[itex]a=const=g[/itex]
integrating with respect to time, [itex]v=gt+v_0[/itex]
Those equations don't take friction into account, so I'm not sure how useful they are. At terminal velocity, velocity is constant and stops changing with respect to time. In that sense, i can see how g is no longer in the equation, but I would like to get a physical understanding of why this is true.
Attempt at a Solution 2
At terminal velocity, the net force on the falling object is zero. The only forces on the system are gravitational force ([itex]F_g=mg[/itex]) and drag force. They must be equal and opposite in magnitude for the sum of net forces to be zero, but that would mean that drag is a function of both mass and gravitational acceleration. This is why I am confused.
*Note: this is "pleasure reading", not a school assignment. I've been stuck on this page for a week and would be grateful for help!