Why Does Gauss' Law Yield Different Results for Spherical Charge Distributions?

[Jelsborg]

Homework Statement

Given charge distribution, electric field and potential, find the total charge between two concentric spheres.

Relevant Equations

V_1(r) = q_0/(4pi*epsilon_0*(r+a))
V_2(r)=(q_0/4pi*epsilon_0*r)*exp(-r/c)

So the first problem stated is to show that for a charge distribution between two spherical shells of radii r1<r2, the total charge inside is described by:

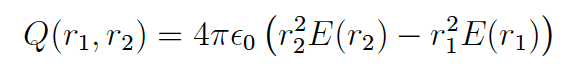
This is rather trivial using Gauss' law in integral form, so I regard this as completed.
I have used the gradient to find the electrical fields (and charge distributions) corresponding to the potentials given in the introduction:

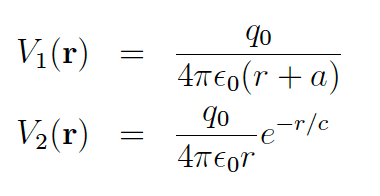
And here comes the part where I get confused.
Using the formula for the total contained charge, I am to examine the total charge enclosed 'in all of space' in the case that r_1 ->0 and r_2 -> infinity for both the electrical fields (as such, obtaining an expression for the total charge by means of Gauss' law in differential form)

Next, I have to calculate the same quantity, only instead I use the integral form of Gauss' law directly on the fields, and then examine what happens as R tends to infinity.

These two methods yield different results, and I am not entirely sure that 1) I'm doing it correctly 2) Why the results differ.

It seems by the way the problem is formulated that the discrepancy is intentional, but I have no idea why.

In case you were wondering, i obtain q0 and -q0 for E1 and E2 respectively when I use the differential form, and q0 and 0 (the discrepancy) for E1 and E2 respectively when I use the integral form.
I really hope someone can help as I've been stuck on this for hours now.

 

[TSny]

To see what's going on, it will help to consider the familiar case where $V = \frac{q_0}{4\pi\epsilon_0 r}$. If you find the total charge "in all of space" using the two different approaches you described, do you get the same result? If not, can you account for the discrepancy for this simple example?

 

[Jelsborg]

To see what's going on, it will help to consider the familiar case where $V = \frac{q_0}{4\pi\epsilon_0 r}$. If you find the total charge "in all of space" using the two different approaches you described, do you get the same result? If not, can you account for the discrepancy for this simple example?

Well yes in that case the first method gives 0, while the second method yields q_0.
Where q_0 is the obvious choice for a right answer. Mathematically it seems pretty obvious why this happens I guess. The physical meaning is where I get lost.

I'm thinking that there's some kind of unfulfilled underlying assumption for one of the methods, which clearly is not valid in this case - I just don't have any idea as to what it is.

 

[TSny]

In this case q_0 seems to be the obvious right answer, since the point charge definitely exists inside 'all of space'

Yes. So, the first method fails to find the point charge at the origin. The first method is based on taking a limit as the radius $r_1$ of the inner spherical surface goes to zero. If you define the function $Q(r_1)$ to be the total charge contained outside a spherical surface of radius $r_1$, then $Q(r_1) = 0$ for any $r_1 > 0$. Method 1 is just taking the limit of $Q(r_1)$ as $r_1 \rightarrow0$.

 

[Jelsborg]

Yes. So, the first method fails to find the point charge at the origin. The first method is based on taking a limit as the radius $r_1$ of the inner spherical surface goes to zero. If you define the function $Q(r_1)$ to be the total charge contained outside a spherical surface of radius $r_1$, then $Q(r_1) = 0$ for any $r_1 > 0$. Method 1 is just taking the limit of $Q(r_1)$ as $r_1 \rightarrow0$.

Since Method 1 in this case yields a negative charge -q0, does that mean that this method fails to find a positive charge q_0 (which was previously the spherical shell of radius r1), thus inferring that the point charge in question is positive?
This would kinda make sense to me as the limit as R -> 0 for the expression in Method 2 yields +q_0

 

[TSny]

Since Method 1 in this case yields a negative charge -q0, does that mean that this method fails to find a positive charge q_0 (which was previously the spherical shell of radius r1), thus inferring that the point charge in question is positive?

Yes. I take it that here you are considering the case $V_2(r)$ of the problem.

This would kinda make sense to me as the limit as R -> 0 for the expression in Method 2 yields +q_0

Right. For very small $r$, $V_2(r)$ is essentially the same as the potential of a single positive point charge $q_0$.

 

[Jelsborg]

Yes. I take it that here you are considering the case $V_2(r)$ of the problem.
Right. For very small $r$, $V_2(r)$ is essentially the same as the potential of a single positive point charge $q_0$.

Yes I am now considering the case $V_{2}(r)$.
So my understanding of this problem is now this:
As $R \rightarrow 0$ in Method 2, this corresponds to the case where the charge density (which is negative) is non-existant as it simply has no volume.
Conversely, letting $r_{1} \rightarrow 0$ and $r_{2} \rightarrow \infty$ in Method 1 is doing the opposite, effectively only counting the volume which contains negative charge density.

Thus, the integral form of Gauss' law seems the most complete, as letting $R \rightarrow \infty$ accounts for all charge

 

[TSny]

Yes I am now considering the case $V_{2}(r)$.
So my understanding of this problem is now this:
As $R \rightarrow 0$ in Method 2, this corresponds to the case where the charge density (which is negative) is non-existant as it simply has no volume.

I'm not quite following this. Method 2 does not involve $R \rightarrow 0$. It involves applying Gauss's law to a sphere of radius $R$ and letting $R \rightarrow \infty$.

We can think of $V_2(r)$ as the potential of a positive point charge at $r = 0$ along with a negative charge density spread throughout all space. The magnitude of the negative charge density is actually very large near $r = 0$. You can work it out using the differential form of Gauss' law. You will see that the negative charge density diverges to negative infinity as $r$ goes to zero. But, nevertheless, the amount of negative charge within a sphere of radius $r_0$ goes to zero as $r_0$ goes to zero due to the fact that the volume of the sphere decreases "faster than the charge density diverges". What this means is that in taking the limits in Method 1, you will account for all of the negative charge (while missing all of the positive charge). But maybe this is what you are saying in the following:

Conversely, letting $r_{1} \rightarrow 0$ and $r_{2} \rightarrow \infty$ in Method 1 is doing the opposite, effectively only counting the volume which contains negative charge density.

Thus, the integral form of Gauss' law seems the most complete, as letting $R \rightarrow \infty$ accounts for all charge

Yes, this sounds good.

 

[Delta2]

I think (not 100% sure) that this discrepancy is due to the discontinuity of charge density(or discontinuity of $\nabla\cdot\vec{E}$) at some points .

 

[TSny]

I think (not 100% sure) that this discrepancy is due to the discontinuity of charge density(or discontinuity of $\nabla\cdot\vec{E}$) at some points .

Yes, $\vec \nabla \cdot \vec E$ does not have a well-defined value at $r = 0$.

$\vec \nabla \cdot \vec E$ has a Dirac delta-function behavior at the origin.