Why Does Increasing Minor Principal Stress Decrease von Mises Stress?

[DTM]

TL;DR

Following the formula for von Mises stress, can you give an intuitive explanation of why the von Mises stress may go down when the minor principal stress goes up.

The formula for von Mises stress for a plane stress (2d) condition with no shear stress is:

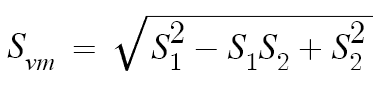
So if S1 = 1000, S2 = 0 , then Svm = 1000.

If the S2 is now increased from 0 to 500. The von Mises stress will go from 1000 to 866

I understand this is how the equation works, but can someone give me an intuitive understanding of why, when you increase a minor principal stress, the von Mises stress (and the likelihood of failure) should go down?

 

[Frabjous]

VM stress is a measure of shear which is a function of the DIFFERENCES of the principal stresses. Don’t forget that the third principal stress is zero.

 

[DTM]

VM stress is a measure of shear which is a function of the DIFFERENCES of the principal stresses. Don’t forget that the third principal stress is zero.

So differences in principal stresses is what makes ductile metals fail. That does make some sense and is somewhat intuitive. Thank you.

 

[Juanda]

Here is a nice video about failure theories which includes Von Mises.



I recommend checking out almost all vídeos from that channel. It's fantastic.

This actually raises the question of why is it that shear stress is responsible for failure in ductile materials while hydrostatic pressure does not contribute. Often textbooks present this kind of information as FACTS because it is not really necessary to know the underlying reasons to be able to squeeze every drop of utility out of a structure by using math.
Since the amount of material to be covered during courses is huge, more often than not these kinds of details are left for the student to research on their own if interested or in separate courses. In my opinion, knowing the experimental and historical context within which such formulas are derived usually helps significantly in their understanding.

Here is some additional info about that hydrostatic pressure scenario and failure modes.

https://physics.stackexchange.com/q...l through shear,move dislocations in this way