- #1
bhanesh
- 9
- 0
Why j.ds has ' closed integral ' on below equation
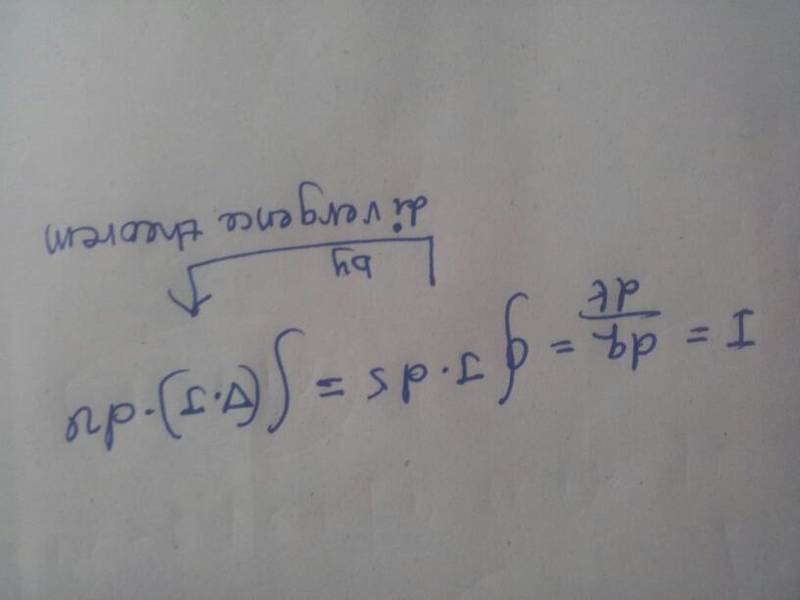
A closed integral on an electromagnetics equation is a mathematical concept that is used to calculate the total amount of a certain physical quantity (such as electric or magnetic field) within a closed surface. It is represented by a symbol that looks like a loop or a circle with an arrow on top, and is often used in Maxwell's equations to describe the behavior of electromagnetic fields.
A closed integral is used in electromagnetics equations because it allows us to calculate the total amount of a physical quantity within a given space, which is important for understanding the behavior and interactions of electromagnetic fields. It is also a useful tool for solving problems in electromagnetics and for predicting the behavior of electromagnetic waves.
One limitation of using a closed integral in electromagnetics equations is that it assumes that the electric and magnetic fields are constant within the closed surface, which may not always be the case. Additionally, it does not take into account the effects of changing electric or magnetic fields over time, which can be important in certain situations.
No, a closed integral is specifically used for calculating the total amount of a vector quantity (such as electric or magnetic field) within a closed surface. It cannot be used for scalar quantities, which do not have a direction associated with them.
A closed integral is used to calculate the total amount of a physical quantity within a closed surface, while an open integral is used to calculate the amount of a physical quantity along a specific path or surface. An open integral is also represented by a different symbol, and is used in different contexts than a closed integral.