Why Does Molecular Potential Energy Curve Have That Specific Shape?

[Dario56]

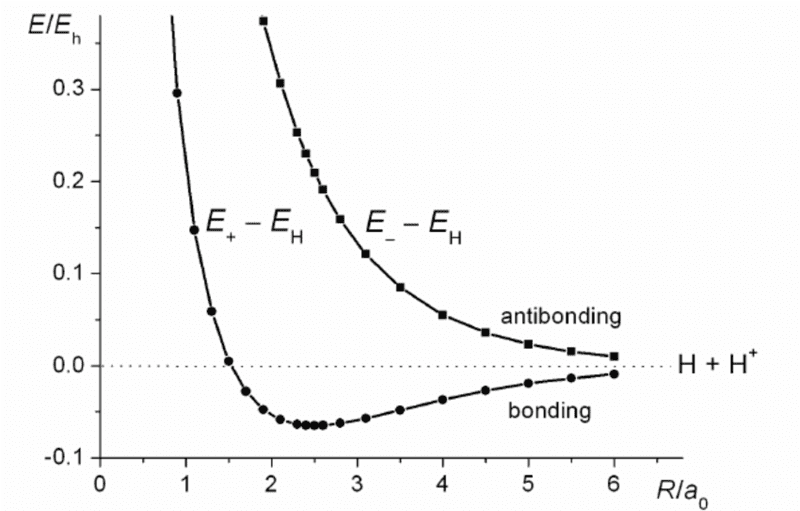
Molecular potential energy of hydrogen in dependence with atomic distance for bonding orbital is given by picture below.

We can see that at large distances force between atoms is attractive and potential energy drops to minimum which corresponds to bond energy and length. This part of the curve looks very similar to interaction between charges of opposite sign at large enough distances (Couloumb interactions)

After that interatomic potential energy starts increasing and at some distance force becomes repulsive.

My question is why does molecular potential energy curve have that shape? Why is it that potential energy first drops to minimum and than starts increasing?

 

[A. Neumaier]

The repulsion force at short distances is due to the Pauli exclusion principle, and the attractive force at long distances is the van der Waals force. You can look up these terms in Wikipedia.

 

[Dario56]

The repulsion force at short distances is due to the Pauli exclusion principle, and the attractive force at long distances is the van der Waals force. You can look up these terms in Wikipedia.

Van der Waals is intermolecular force and here we are talking about chemical bonds.

 

[gentzen]

Van der Waals is intermolecular force and here we are talking about chemical bonds.

But A. Neumaier might be right nevertheless. At large distances, each H has an electron and so forms an electrically neutral "molecular" unit. The attractive force between these units might best be described as the van der Waals force.

 

[Dario56]

But A. Neumaier might be right nevertheless. At large distances, each H has an electron and so forms an electrically neutral "molecular" unit. The attractive force between these units might best be described as the van der Waals force.

Yes, that is a valid point. Why is it that potential energy firstly decreases and than starts to increase?

 

[A. Neumaier]

Van der Waals is intermolecular force and here we are talking about chemical bonds.

At large distance there are no chemical bonds. The curves you drew have for neutral atoms a large distance dependence proportional to $r^{-6}$, which is the van der Waals contribution. Maybe because of the ionic part it is proportional to $r^{-4}$ due to dipolar forces.

https://scholar.google.com/scholar?&q=diatomic+potentials

 

[Dario56]

At large distance there are no chemical bonds. The curves you drew have for neutral atoms a large distance dependence proportional to $r^{-6}$, which is the van der Waals contribution. Maybe because of the ionic part it is proportional to $r^{-4}$ due to dipolar forces.

https://scholar.google.com/scholar?&q=diatomic+potentials

While it is true that chemical bonds don't occur at large distances, Van der Waals is really an intermolecular force and not intramolecular. Since here we are looking at two hydrogen atoms, Van der Waals force can't be the cause of interatomic interaction and consequently chemical bonding. Van der Waals forces are much weaker than interatomic interactions or chemical bonds and so it makes no sense to me that they can cause chemical bonding since how can we explain difference in strength of intermolecular and interatomic interactions? Also, Van der Waals forces between two hydrogen atoms could only be due to randomly induced dipoles in the atoms which is known as the least strong interaction even for intermolecular interactions.

 

[Motore]

While it is true that chemical bonds don't occur at large distances, Van der Waals is really an intermolecular force and not intramolecular.

Not acording to:
https://en.wikipedia.org/wiki/Van_der_Waals_force

 

[Dario56]

Not acording to:
https://en.wikipedia.org/wiki/Van_der_Waals_force

Here is a quote from wikipedia: "a distance-dependent interaction between atoms or molecules. Unlike ionic or covalent bonds, these attractions do not result from a chemical electronic bond; they are comparatively weak and therefore more susceptible to disturbance."

While wikipedia article states that it is both an intermolecular and intramolecular interaction, in the next sentence it is said that Van der Waals is unlike ionic or covalent bond since it has different origin.

 

[A. Neumaier]

Here is a quote from wikipedia: "a distance-dependent interaction between atoms or molecules. Unlike ionic or covalent bonds, these attractions do not result from a chemical electronic bond; they are comparatively weak and therefore more susceptible to disturbance."

While wikipedia article states that it is both an intermolecular and intramolecular interaction, in the next sentence it is said that Van der Waals is unlike ionic or covalent bond since it has different origin.

Ionic bonds are due to Coulomb forces which are $O(r^{-1}$. Covalent bonds are due to forming electron pairs, but these forces are also short range. You need quantum chemistry (at least Hartree-Fock) to understand how the corresponding forces arise.

 

[Dario56]

Ionic bonds are due to Coulomb forces which are $O(r^{-1}$. Covalent bonds are due to forming electron pairs, but these forces are also short range. You need quantum chemistry (at least Hartree-Fock) to understand how the corresponding forces arise.

Yes, in our example we have two hydrogen atoms forming covalent bond. I am interested in what causes attractive force in bonding orbital. Repulsive force is Pauli exclusion principle, but what about attrative force?

 

[hutchphd]

The only force in the problem that matters is coulomb force which, since there are two different kinds of charges present in this complicated multibody problem, can have either sign. The assignment of the other named forces is simply shorthand for the various mathematical fictions we create to make the calculation tractable.
Some of these forces (Van der Waals and ionic) are essentially classical and the "exchange" interactions are decidedly not. The level of understanding you obtain is determined by how carefully you wish to do the calculations. The devil is in the detail.

 

[Dario56]

The only force in the problem that matters is coulomb force which, since there are two different kinds of charges present in this complicated multibody problem, can have either sign. The assignment of the other named forces is simply shorthand for the various mathematical fictions we create to make the calculation tractable.
Some of these forces (Van der Waals and ionic) are essentially classical and the "exchange" interactions are decidedly not. The level of understanding you obtain is determined by how carefully you wish to do the calculations. The devil is in the detail.

Yes, this is actually what I thought initially. There are charges in atoms which interact by couloumb force and on the level of two atoms, this force is attractive. When atoms get really close, repulsive force becomes significant because of Pauli exclusion principle. Did I explain this correctly?

 

[gentzen]

Yes, this is actually what I thought initially. There are charges in atoms which interact by couloumb force and on the level of two atoms, this force is attractive. When atoms get really close, repulsive force becomes significant because of Pauli exclusion principle. Did I explain this correctly?

So you mean that the repulsive forces become significant because the two positively charged atoms repel each other, independent of Pauli exclusion principle.

 

[Dario56]

So you mean that the repulsive forces become significant because the two positively charged atoms repel each other, independent of Pauli exclusion principle.

No, I think Pauli exclusion is the reason why potential energy curve starts increasing.

 

[gentzen]

No, I think Pauli exclusion is the reason why potential energy curve starts increasing.

So for two different atoms like H and Li, the potential curve would not start increasing? And for two neutrons, the curve would start increasing at a similar distance as seen above?

 

[Dario56]

So for two different atoms like H and Li, the potential curve would not start increasing? And for two neutrons, the curve would start increasing at a similar distance as seen above?

Why wouldn't it start increasing?

 

[A. Neumaier]

So for two different atoms like H and Li, the potential curve would not start increasing? And for two neutrons, the curve would start increasing at a similar distance as seen above?

The repulsion results from the exclusion principle for the electrons, which are identical no matter which nucleus. The Coulomb repulsion between the nuclei matters only if the nuclei are extremely close.

The increase results from the superposition of the repulsive force with an attractive covalent binding force whose origin is the favorable energy balance when an electron pair with two opposite spins forms.

 

[gentzen]

The repulsion results from the exclusion principle for the electrons, which are identical no matter which nucleus. The Coulomb repulsion between the nuclei matters only if the nuclei are extremely close.

I would agree that the difference between the curves for bonding and antibonding is caused by the exclusion principle for the electrons. For the bonding case, the two electrons have different spin, so the exclusion principle doesn't affect them.

But the Coulomb repulsion between the nuclei should get significant when the nuclei are so close together that the electrons can no longer efficiently shield their Coulomb interaction. And I would not call that extremely close.

 

[Twigg]

While it is true that chemical bonds don't occur at large distances, Van der Waals is really an intermolecular force and not intramolecular.

Why not both? In practice, all "Van der Waals" force really means is an electromagnetic force that occurs between two polarizable bodies due to their induced dipole moments, or due to an induced dipole moment interacting with a permanent dipole moment. The physics doesn't care if the polarizable bodies are atoms, molecules, or mackerel. It just so happens that the VdW force is negligible for macroscopic objects. If you're not convinced, try reading the wikipedia on Lennard-Jones potential, noting that dispersion forces are just a subset of VdW interactions.

 

[Dario56]

Why not both? In practice, all "Van der Waals" force really means is an electromagnetic force that occurs between two polarizable bodies due to their induced dipole moments, or due to an induced dipole moment interacting with a permanent dipole moment. The physics doesn't care if the polarizable bodies are atoms, molecules, or mackerel. It just so happens that the VdW force is negligible for macroscopic objects. If you're not convinced, try reading the wikipedia on Lennard-Jones potential, noting that dispersion forces are just a subset of VdW interactions.

Agree with that. However, this force can't be the main source of bonding between atoms since interaction between atoms would be weak if only such interactions existed between them or in another words if only vdW dictated chemical bonding than it would be impossible to explain how are chemical bonds much stronger than intermolecular interactions.

 

[Twigg]

impossible to explain how are chemical bonds much stronger than intermolecular interactions.

Isn't that just an issue of length scales? It's a short range force.

 

[timmdeeg]

The physics doesn't care if the polarizable bodies are atoms, molecules, or mackerel

or geckos.

 

[A. Neumaier]

I would agree that the difference between the curves for bonding and antibonding is caused by the exclusion principle for the electrons. For the bonding case, the two electrons have different spin, so the exclusion principle doesn't affect them.

But the Coulomb repulsion between the nuclei should get significant when the nuclei are so close together that the electrons can no longer efficiently shield their Coulomb interaction. And I would not call that extremely close.

Quantum mechanical calculations by

• R.K. Pathak and A.J. Thakkar, Very short-range interatomic potentials, J. Chem. Phys. 87 (1987), 2186--2190.

show that the correct asymptotics at very short-range is $O(r^{-1})$, corresponding to Coulomb repulsion. Nevertheless, repulsive exchange forces are often taken to be $O(r^{-12})$ which is much more, though this is wrong at very small $r$ - much smaller than what is accessible at chemically relevant energies.

 

[A. Neumaier]

In practice, all "Van der Waals" force really means is an electromagnetic force that occurs between two polarizable bodies due to their induced dipole moments, or due to an induced dipole moment interacting with a permanent dipole moment.

No. This gives stronger $O(r^{-4})$ attraction, whereas van der Waals has weaker $O(r^{-6})$ attraction, also present for nonpolar atoms, e.g., in Argon clusters.

this force can't be the main source of bonding between atoms

Argon clusters are molecules only bound by noncovalent van der Waals forces.

Covalent bounds are much stronger since electron pairs form, which are energetically much more favorable. You really need some quantum chemistry to understand this!

 

[Twigg]

My understanding was induced dipole - induced dipole goes like $r^{-6}$, and induced dipole - permanent dipole goes like $r^{-4}$, but both fall under the umbrella of van der Waals interactions. I might have my jargon off, sorry about that.

 

[A. Neumaier]

My understanding was induced dipole - induced dipole goes like $r^{-6}$, and induced dipole - permanent dipole goes like $r^{-4}$, but both fall under the umbrella of van der Waals interactions. I might have my jargon off, sorry about that.

van der Waals is a pure quantum effect also present between nonpolar atoms (inert gases).