greg_rack
Gold Member
- 361
- 79
- Homework Statement
- $$\int \frac{lnx}{(x+1)^2} dx$$
- Relevant Equations
- none
Hi guys,
I've attempted to integrate this function by parts, which seemed to be the most appropriate method... but apparently, I'm getting something wrong since the result doesn't match the right one.
Everything looks good to me, but there must be something silly missing :)
My attempt:
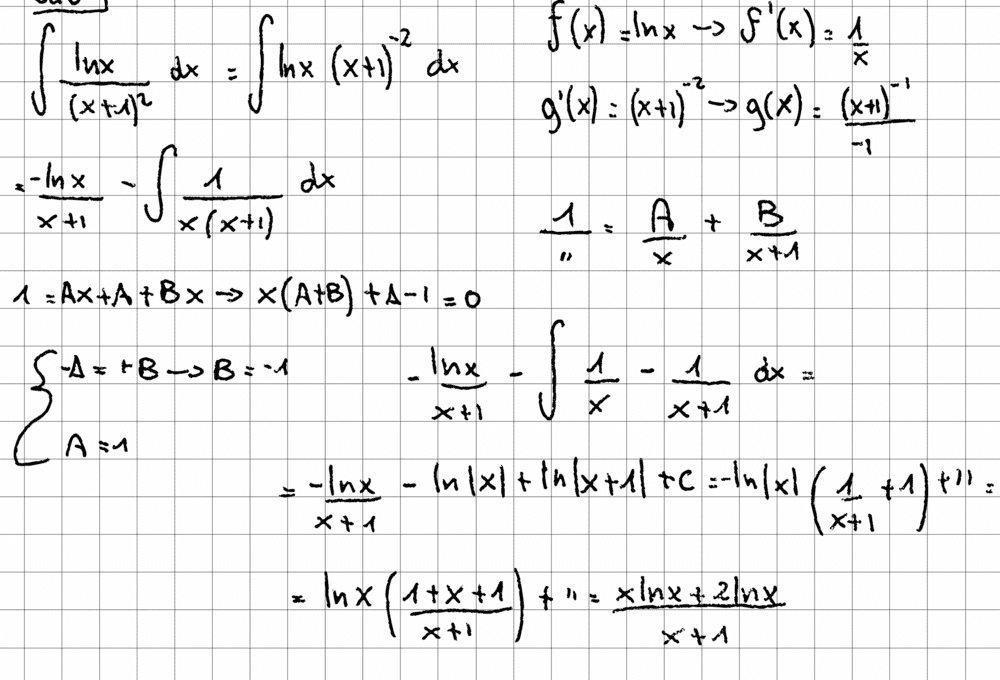
I've attempted to integrate this function by parts, which seemed to be the most appropriate method... but apparently, I'm getting something wrong since the result doesn't match the right one.
Everything looks good to me, but there must be something silly missing :)
My attempt: