chriswong
- 2
- 0
Summary:: Stoke stream function
[Mentor Note -- Thread moved from the technical forums, so no Homework Template is shown]
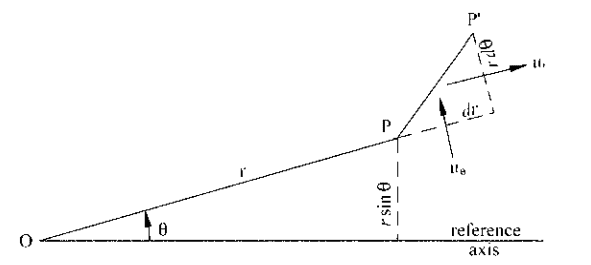
Why the quantity of fluid that crosses the surface of revolution formed by the vector OP is
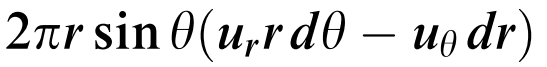 ?
?
[Mentor Note -- Thread moved from the technical forums, so no Homework Template is shown]
Why the quantity of fluid that crosses the surface of revolution formed by the vector OP is
Last edited by a moderator: