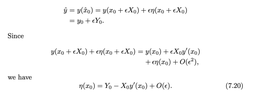Why Does Taylor's Theorem Use +O(ε) Instead of -O(ε)?

[gionole]

Homework Statement

Help me with taylor's theorem

Relevant Equations

Help me with taylor's theorem

I am trying to grasp how the last equation is derived. I understand everything, but the only thing problematic is why in the end, it's $+O(\epsilon)$ and not $-O(\epsilon)$. It will be easier to directly attach the image, so please, see image attached.

 

[anuttarasammyak]

I am not accustomed the way of the text. What is the text you use ?

 

[pasmith]

O-notation tells you about the magnitude of the error in some limit, in this case \epsilon \to 0; the sign of the error can depend on \epsilon, so it is conventional to use a plus sign.

 

[Hill]

The expression, $f=g+O(\epsilon)$ means that there exists such positive number $M$ that $|f-g| \leq M|\epsilon|$.
OTOH, $f=g-O(\epsilon)$ means $g=f+O(\epsilon)$, which means that there exists such positive number $M$ that $|g-f| \leq M|\epsilon|$. This is the same as above. So, one can always use $+O(\epsilon)$.