Why Does Tension Act in Two Directions at a Point in a String?

[andyrk]

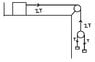
Why is tension at a specific point in a string in 2 directions? For example in the first part of image 1, the string is pulling the two blocks upwards. And in the second part of image 1, the string is pulling the pulley down too. Does tension at a point in a string try to pull the point in 2 directions?

And in image 2, why is the bottom most pulley (which is not hinged) pulled up by a tension 2T? If it is, that means there is no net force acting on it but then how is it moving down if there is no force on it? No force means no acceleration but still it can have a constant velocity (no acceleration) with which it moves down. But why and how does it get that velocity?

 

[Bystander]

Does tension at a point in a string try to pull the point in 2 directions?

Hold one end of a string in one hand. Apply a tension. How taut is the string? Hold one end of the same string in one hand, and the second end in the other and pull in opposite directions. How taut is the string? Can you apply tension by pulling on only one end?

pulled up by a tension 2T?

The diagram shows two masses of 1 T hanging from the pulley by a string run over the pulley. Two times one is two.

how is it moving down

It's not.

 

[andyrk]

Hold one end of a string in one hand. Apply a tension. How taut is the string? Hold one end of the same string in one hand, and the second end in the other and pull in opposite directions. How taut is the string? Can you apply tension by pulling on only one end?

The diagram shows two masses of 1 T hanging from the pulley by a string run over the pulley. Two times one is two.

It's not.

Right, for a string to have tension or remain taut, it needs to be connected or pulled from both ends with equal force.

But shouldn't it move down? Why should there be no forces on the unhinged pulley?

 

[haruspex]

Right, for a string to have tension or remain taut, it needs to be connected or pulled from both ends with equal force.

But shouldn't it move down? Why should there be no forces on the unhinged pulley?

Your second diagram lacks important information about masses and friction. Is there some accompanying text you've omitted?

 

[Bystander]

be no forces on the unhinged pulley?

Two T down, and two T up --- no indication in the diagram that the block anchoring the upper string is moving/sliding on the table top. The string supporting the lower pulley is NOT wrapped around the pulley, or turning it --- it's not shown specifically in the diagram, but in the real world, it would be attached to a clevis which carries the shaft around which the pulley turns.

 

[andyrk]

Your second diagram lacks important information about masses and friction. Is there some accompanying text you've omitted?

Nope. I just wanted to know that why is the unhinged pulley being pulled by a tension 2T upwards?

 

[haruspex]

Nope. I just wanted to know that why is the unhinged pulley being pulled by a tension 2T upwards?

how do you know that it is, other than that someone has drawn it on the diagram?

 

[andyrk]

Because that's what the solution I am looking at says.

I didn't mention some facts which were also included in the question-
1.No frictional forces
2. Massless pulleys and strings

Does that somehow help you to give a reasoning as to why the pulley is being pulled up by tension 2T?

 

[haruspex]

Because that's what the solution I am looking at says.

I didn't mention some facts which were also included in the question-
1.No frictional forces
2. Massless pulleys and strings

Does that somehow help you to give a reasoning as to why the pulley is being pulled up by tension 2T?

That's why I asked about further information!
If an object is massless then it doesn't matter whether it is accelerating or not. $\Sigma F = ma$ tells you that the net force must be zero.

 

[andyrk]

Oops..sorry my bad. But how is it still moving down then?

 

[haruspex]

Oops..sorry my bad. But how is it still moving down then?

I presume the three blocks have mass, so there should be the weights of the two smaller blocks acting down. It will turn out that these are less than 2T in sum, so those blocks will accelerate downwards. Since the strings do not break, they and the pulley must accelerate down too.

 

[andyrk]

The 2T up and the two Ts down cancel out. So by the virtue of which force does the pulley move down?

 

[haruspex]

The 2T up and the two Ts down cancel out. So by the virtue of which force does the pulley move down?

Like I said, the pulley has no mass, so it needs no force to accelerate which ever way. Its motion is determined by whatever it is attached to.
To make it more realistic, you could let the pulley have a very small mass. When you work out the whole system you will now find that the tensions down slightly exceed the tension up, giving the pulley just the acceleration it needs to keep all the strings taut. The same applies to the strings themselves, etc.
The 'massless' fiction just means the mass is insignificant compared with the other masses in the system.

 

[andyrk]

What? Why? The tensions down always equal the tension up. How can they be slightly greater than the upper tension?

 

[haruspex]

What? Why? The tensions down always equal the tension up. How can they be slightly greater than the upper tension?

Actually I got it backwards - forgot gravity. The tension up will exceed tension down.
The system is accelerating. If the pulley has mass then there must be a net force to accelerate it downwards. The acceleration will be less than g, so the net of the tensions must be upwards.

 

[andyrk]

So if the net of the tensions is upwards then would the pulley start moving upwards instead of downwards?

 

[haruspex]

So if the net of the tensions is upwards then would the pulley start moving upwards instead of downwards?

No, you've forgotten gravity acting on the pulley (as I did). The net force on the pulley will be downwards, accelerating it down at the same rate as the rest of the system. But that rate is less than g, so the net force of the strings must be upwards.

 

[andyrk]

But for the pulley to move down, why does need to have greater upper tension than lower? Even if they are same, pulley can still move down because of its mass. So why do the upper and lower tensions need to be different?

 

[haruspex]

for the pulley to move down, why does need to have greater upper tension than lower?

That's not what I said.
For the pulley to accelerate down, the net force must be downwards: tensions down + mg > tension up. But the system will accelerate at a rate less than g, and for that reason tensions down < tensions up.

 

[andyrk]

That's not what I said.
For the pulley to accelerate down, the net force must be downwards: tensions down + mg > tension up. But the system will accelerate at a rate less than g, and for that reason tensions down < tensions up.

If tensions down = tensions up still, tensions down + mg > tension up. So why is tensions down < tensions up?

 

[haruspex]

If tensions down = tensions up still, tensions down + mg > tension up. So why is tensions down < tensions up?

The downward acceleration will be < g, so the net downward force must be < mg. T_down+mg-T_up < mg. T_down<T_up .

 

[andyrk]

The downward acceleration will be < g, so the net downward force must be < mg. T_down+mg-T_up < mg. T_down<T_up .

I didn't get the inequalities you just showed. Can you explain them once again?
Why should T_down+mg-T_up be < mg? Is there any reason for it?

 

[haruspex]

I didn't get the inequalities you just showed. Can you explain them once again?
Why should T_down+mg-T_up be < mg? Is there any reason for it?

Let the mass of the pulley be m and the acceleration of the system (i.e. all the bits that move) be a. Do you agree they will all have the same acceleration? Do you see why a < g?
For the pulley, T_down+mg-T_up = ma < mg.

 

[Chestermiller]

If the two masses are moving down, then T < mg. Then, if the pulley is massless, the 2T = T + T. So, the 2T < 2mg.

Is this what you were saying, andyrk? If so, then I agree.

Chet

 

[andyrk]

That's why I asked about further information!
If an object is massless then it doesn't matter whether it is accelerating or not. $\Sigma F = ma$ tells you that the net force must be zero.

But wait, why would the pulley be pulled by two forces T and T in the downward direction on either side of the pulley in the first place? Shouldn't the points at which the pulley is being pulled downwards by T also be pulled upwards by T (since tension at a point acts in two directions), such that effectively the pulley isn't being pulled down at all and so we don't need the 2T force to exist? But this is not the case as we see in the image in post #1. Can somebody explain this?

 

[haruspex]

But wait, why would the pulley be pulled by two forces T and T in the downward direction on either side of the pulley in the first place? Shouldn't the points at which the pulley is being pulled downwards by T also be pulled upwards by T (since tension at a point acts in two directions), such that effectively the pulley isn't being pulled down at all and so we don't need the 2T force to exist? But this is not the case as we see in the image in post #1. Can somebody explain this?

In reality, the rope exerts a radial force on the pulley at all points where it contacts the pulley. But that makes it rather complicated to analyse, so typically you treat the part of the rope in contact with the pulley as part of the pulley. Now it's easy, the straight part exerts a pull T on the end of the curved part.

 

[andyrk]

In reality, the rope exerts a radial force on the pulley at all points where it contacts the pulley. But that makes it rather complicated to analyse, so typically you treat the part of the rope in contact with the pulley as part of the pulley. Now it's easy, the straight part exerts a pull T on the end of the curved part.

But that T is in two opposite directions right?

 

[haruspex]

But that T is in two opposite directions right?

Yes, but that's normal action and reaction. The straight section of rope pulls on the curved part+pulley, while the curved part+pulley pulls on the straight section.

 

[andyrk]

Yes, but that's normal action and reaction. The straight section of rope pulls on the curved part+pulley, while the curved part+pulley pulls on the straight section.

Oh. So the two T's don't act on the pulley itself? Only the upper one does? So why doesn't it happen the other way round? That is, why doesn't the curved part + pulley pull the straight part up and the straight part pulls the curved part + pulley down? So that the two T's instead of being down are up?

 

[andyrk]

I see, the 2T tension in the upper string would also reverse its direction in that case. Either way, either the two tensions acting on the pulley are down or u but not both. Am I right? And the 2T tension above adjusts its direction accordingly. Right?

 

[Chestermiller]

I see, the 2T tension in the upper string would also reverse its direction in that case. Either way, either the two tensions acting on the pulley are down or u but not both. Am I right? And the 2T tension above adjusts its direction accordingly. Right?

You are aware that when you have an action-reaction pair at the contact point between two bodies A and B, one member of the pair is the force exerted by body B on body A, and the other member of the pair is the force exerted by body A on body B, correct? When you are doing a force balance on body A, the two don't cancel. The force balance on body A includes only forces exerted by other bodies on body A, and not forces exerted by body A on other bodies. If both members of an action-reaction pair always had to be included, then no body could ever exert a force on any other body.

Can you see how this all relates to your rope and pulley?

Chet

 

[andyrk]

You are aware that when you have an action-reaction pair at the contact point between two bodies A and B, one member of the pair is the force exerted by body B on body A, and the other member of the pair is the force exerted by body A on body B, correct? When you are doing a force balance on body A, the two don't cancel. The force balance on body A includes only forces exerted by other bodies on body A, and not forces exerted by body A on other bodies. If both members of an action-reaction pair always had to be included, then no body could ever exert a force on any other body.

Can you see how this all relates to your rope and pulley?

Chet

So is the action reaction logic the reason why a point in a rope has tensions in two opposite directions all throughout the rope? And if that is the case then why does the end of the string still have tension T while the block is pulling the string down with force m₁g on one end and m₂g on the other end?

 

[Chestermiller]

So is the action reaction logic the reason why a point in a rope has tensions in two opposite directions all throughout the rope?

Suppose you have a rope under tension T (with both of its ends fixed), and you decide to cut the rope at a certain location. Say the rope is horizontal, and, after you cut it, you have a left section and a right section. You decide what you are going to do is, by hand, replace the force that the right section was exerting on the left section, so that the tension within the left section is the same as it was before. What force would you have to apply by hand to accomplish this? What direction would this force be pointing?

Now you decide to do the same thing with the right section, rather than the left section. What force would you have to apply by hand to the right section so that it is under the same tension as before? What direction would this force be pointing?

Chet

 

[andyrk]

Suppose you have a rope under tension T (with both of its ends fixed), and you decide to cut the rope at a certain location. Say the rope is horizontal, and, after you cut it, you have a left section and a right section. You decide what you are going to do is, by hand, replace the force that the right section was exerting on the left section, so that the tension within the left section is the same as it was before. What force would you have to apply by hand to accomplish this? What direction would this force be pointing?

Now you decide to do the same thing with the right section, rather than the left section. What force would you have to apply by hand to the right section so that it is under the same tension as before? What direction would this force be pointing?

Chet

For the left section, I would have to apply the same force that the right section was pulling it with when it was not cut. And for the right section, I would have to apply the same force that the left section was pulling it with when it was not cut. But whether the two forces are equal or not is still unclear.

 

[Chestermiller]

For the left section, I would have to apply the same force that the right section was pulling it with when it was not cut. And for the right section, I would have to apply the same force that the left section was pulling it with when it was not cut. But whether the two forces are equal or not is still unclear.

If you go around to the other side of the string, the left side becomes the right side, and right side becomes the left side. So the forces have to be the same, since the place where you personally are located can't affect the string.

Chet