Why does the current have no ##\phi## component in a toroidal coil?

[Adesh]

These are images from the book Introduction to Electrodynamics by David J. Griffiths .

.

.

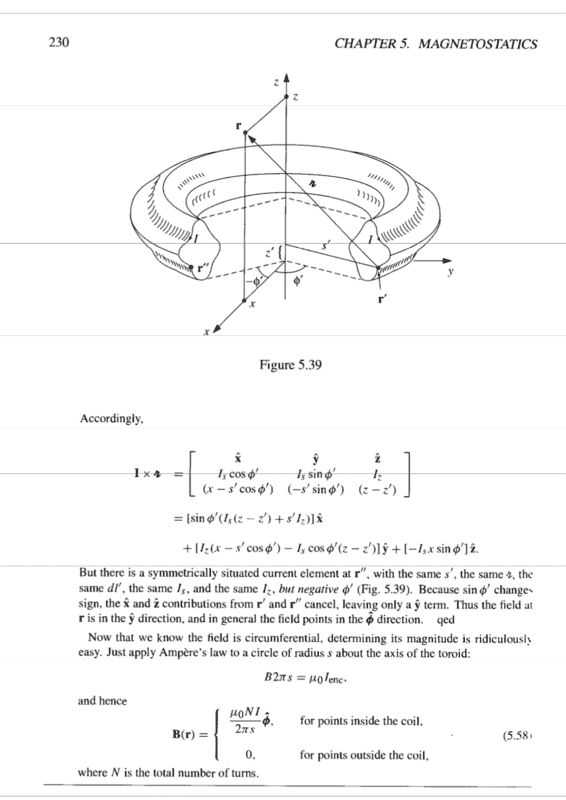My problem is that I'm unable to understand how the current has zero $\phi$ component (I have underlined it in the first image)? I do understand cylindrical coordinates, I know cylindrical coordinates involve three components $(r,ϕ,z)$and $\hat{r}$r^ points radially outwards, $\hat{\phi}$ points perpendicular to $\hat{r}$ and even to $z$ axis.

I fully understand this image (credit: https://physics.stackexchange.com/users/110781/frobenius)

.

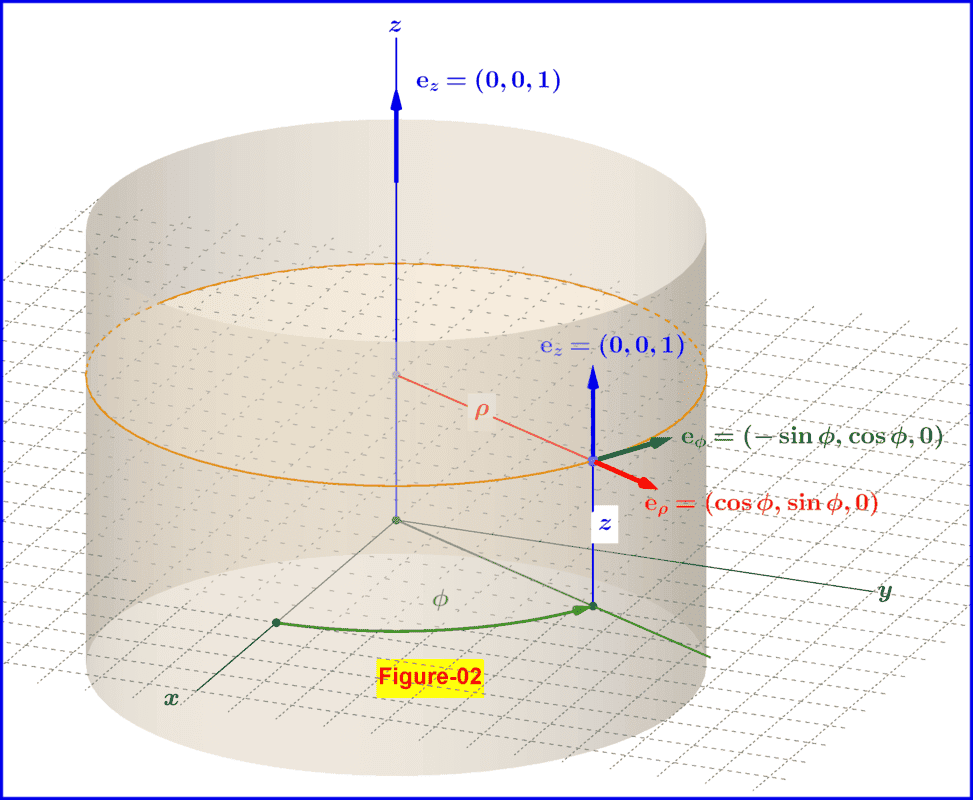But in spite of all these I can't seem to understand how the current have no $\phi$ component. Well, in that toroid we have current going on in circles and really I don't anything more than this.

Please help me!

 

[Charles Link]

There will always be a $\phi$ component of $I$ from the toroid, but if $n=N/L$ is made very large, then the toroid current $I$ can be minimized. This step is really necessary, because it really simplifies things.

 

[Dale]

It is just an approximation/simplification

 

[Adesh]

It is just an approximation/simplification

Can you please make a figure and show me what really happens when we increase number of turns per unit length too much.

 

[Charles Link]

Theoretically, we can also make the wire as fine as possible. The result is a current per unit length exactly how it is modeled, without any $\phi$ component, with $n=N/L \rightarrow + \infty$, and $I \rightarrow 0$, and finite current per unit length $K=n I$.

 

[Dale]

Can you please make a figure and show me what really happens when we increase number of turns per unit length too much.

I cannot, I am not that good of an artist.

 

[Adesh]

Theoretically, we can also make the wire as fine as possible. The result is a current per unit length exactly how it is modeled, without any $\phi$ component, with $n=N/L \rightarrow + \infty$, and $I \rightarrow 0$, and finite current per unit length $K=n I$.

I request you to please explain me how $n \to \infty$ implies $I \to \infty$.

 

[sysprog]

In my view, trying to model the toroid without the triple integral (1 integral for each dimension), means that you're probably trying to model it as a disc -- that's possibly a mistake -- I'm presently too lazy to do the proof . . .

 

[Adesh]

means that you're probably trying to model it as a disc -- that's possibly a mistake --

How to picture it?

Well, I’m ready to do everything. Just tell me, just give me directions :-)

 

[sysprog]

How to picture it?

Well, I’m ready to do everything. Just tell me, just give me directions :-)

Nice eager attitude, but are you ready for triple integrals? If you haven't yet become comfortable with single variable calculus, you probably aren't yet ready . . .

 

[Adesh]

Nice eager attitude, but are you ready for triple integrals? If you haven't yet become comfortable with single variable calculus, you probably aren't yet ready . . .

Well, I know Multivariable Calculus. Once I got a problem about finding the volume between the intersection of three orthogonal cylinders which took me 2 weeks, finally I took help from @Charles Link for that.

So, in short I’m ready for the drill !

 

[Vanadium 50]

This thread is a mess.

I refer to the first drawing. The other two seem unrelated to the problem.

There is no calculus required. There is no current in the phi direction because the problem defines it that way. Look at the drawing: the wires go up in z, in in r, down in z, and out in r. They do not go in phi at all. Since the wires don't go in phi, neither does the current.

If you want to argue that this is an approximation of a physical toroid, we can go down that route, but that is not the problem as asked.

 

[PeroK]

How to picture it?

Well, I’m ready to do everything. Just tell me, just give me directions :-)

Let's consider a single electron. Let's say it takes $1s$ to go round one loop of the wire. If there are $n$ loops of wire, then it takes $n$ seconds to travel all the way round the torus. The current in the $r-z$ circumferential direction is, therefore, $n$ times the current in the $\phi$ direction.

If $n$ is large enough, therefore, the $\phi$ current is negligible.

Now, time to move on to the problem at hand.

 

[Adesh]

This thread is a mess.

I refer to the first drawing. The other two seem unrelated to the problem.

There is no calculus required. There is no current in the phi direction because the problem defines it that way. Look at the drawing: the wires go up in z, in in r, down in z, and out in r. They do not go in phi at all. Since the wires don't go in phi, neither does the current.

If you want to argue that this is an approximation of a physical toroid, we can go down that route, but that is not the problem as asked.

But in the second figure (where the cross-sectional area is weird) I’m having trouble in seeing how it doesn’t have a phi component.

You have made it very clear to me about how phi component is zero in the first figure.

 

[Vanadium 50]

I got your PM. I do not owe you an explanation when you demand it, and certainly not in less than 24 hours. I will not be participating in this thread any more.

 

[sysprog]

I intended to show how to determine the volume of each loop of the wire, along with the volume of the toroid, (and then take it from there to Maxwell's for the induction) -- that's where I was going with the triple integrals and other things -- but I was redirected by someone (@Vanadium 50, who knows his stuff and thousands of times has graciously shared his knowledge, thinking, and understanding) letting me know that all that wasn't necessary, and on reflection, I think that he was definitely right.

 

[Adesh]

I intended to show how to determine the volume of each loop of the wire, along with the volume of the toroid, (and then take it from there to Maxwell's for the induction) -- that's where I was going with the triple integrals and other things -- but I was redirected by someone (@Vanadium 50, who knows his stuff and thousands of times has graciously shared his knowledge, thinking, and understanding) letting me know that all that wasn't necessary, and on reflection, I think that he was definitely right.

Since he has sworn not to come back here, can we follow your route or any other body’s ?

 

[sysprog]

Since he has sworn not to come back here, can we follow your route or any other body’s ?

@Vanadium 50 didn't swear to do or not do anything here; he just said he was done in this thread; he probably won't change his mind about that, but I think that he's at liberty to do so; as for the question, he already schooled me about that, so, no, I won't be playing math boy in this thread, but that's not a sworn statement.

 

[Adesh]

@Vanadium 50 didn't swear to do or not do anything here; he just said he was done in this thread; he probably won't change his mind about that, but I think that he's at liberty to do so; as for the question, he already schooled me about that, so, no, I won't be playing math boy in this thread, but that's not a sworn statement.

All right, no problem!

 

[PeroK]

Since he has sworn not to come back here, can we follow your route or any other body’s ?

Is there another question about the problem? The matter of (approx) zero current in the $\phi$ direction must be settled now, surely?

 

[sysprog]

Is there another question about the problem? The matter of (approx) zero current in the $\phi$ direction must be settled now, surely?

In my opinion, yes, the answers of @Vanadium 50 settled that -- I wanted to hold forth about centroids and such, and he gently settled my hash . . .

 

[hutchphd]

Is the issue that the windings have a slight (nonzero) pitch? Jeez, just wind two layers, one "around the donut" and one "back". Zero pitch.

 

[Adesh]

Is there another question about the problem? The matter of (approx) zero current in the $\phi$ direction must be settled now, surely?

Thanks for asking me :-)

Actually, if you look at that example, Griffiths is explaining everything with the help of that 2nd figure (that weird cross sectional area in the 1st post) so it was quite obvious for me to take his words “the $\phi$ component of the current is zero” for that 2nd figure.

I want to know is the $\phi$ current zero in that 2nd figure (of my first post)?

 

[Adesh]

Is the issue that the windings have a slight (nonzero) pitch? Jeez, just wind two layers, one "around the donut" and one "back". Zero pitch.

I want to know is the $\phi$ component of current is zero even in that 2nd figure?

 

[sysprog]

People sometimes use 'zero' when they mean 'negligibly different from zero'.

 

[hutchphd]

I suppose there is a reason for the weird cross-section shape ...maybe this is a fusion " tokamak' coil and you want some lensing? Some one must know (not me) . But it still clearly is toroidally wound.

 

[Adesh]

I suppose there is a reason for the weird cross-section shape ...maybe this is a fusion " tokamak' coil and you want some lensing? Some one must know (not me) . But it still clearly is toroidally wound.

When the cross section is rectangular I can see that $\phi$ current is zero.

But now let’s imagine, we got a slinky and we join it end to end to form a toroid, now since the cross-sectional area is circular then definitely we have a $\phi$ component. Even if the turns are so close to each other then also we have a circular cross-sectional area, and a circle’s line element does involve a $\phi$ component.

 

[hutchphd]

Yes it likely will have a very very small phi component but it could be wound in such a way that it was actually zero in the unlikely event it really mattered. Nothing is ever perfectly exact!

 

[Adesh]

Yes it likely will have a very very small phi component but it could be wound in such a way that it was actually zero in the unlikely event it really mattered. Nothing is ever perfectly exact!

Can you please draw a figure (or at least guide me) to show how it got a negligible $\phi$ component? I’m really unable to see it.

 

[Adesh]

Here are two figures that I tried to draw