Darkmisc
- 222
- 31
- Homework Statement
- Prove that the medians bisecting the equal sides of an isosceles triangle are equal.
- Relevant Equations
- a · b = |a| × |b| × cos(θ)
a · b = ax × bx + ay × by
Hi everyone
I have the solutions for the problem. It makes sense except for one particular step.
Why does the dot product of a and b equal zero? I thought this would only be the case if a and b were at right angles to each other. The solutions seem to be a general proof and should work for all isosceles triangles (not just right angle triangles).
The solution would still make sense even if a · b didn't equal zero. Why does it equal zero here?
Thanks
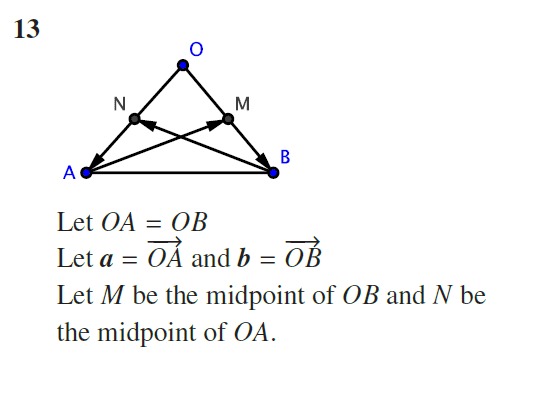
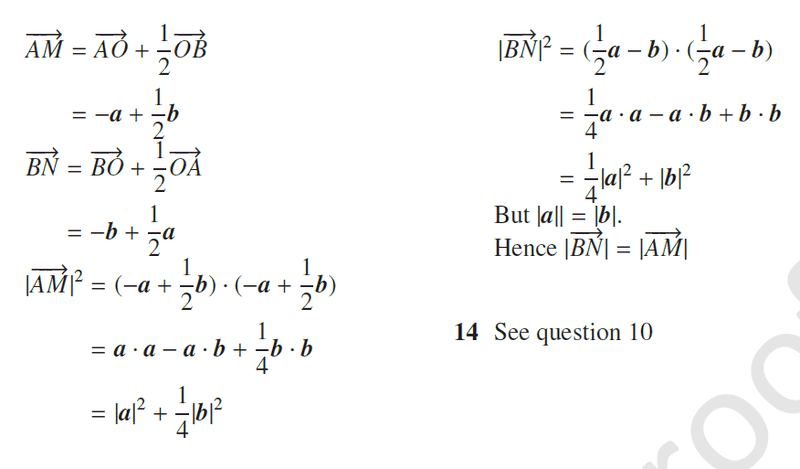
I have the solutions for the problem. It makes sense except for one particular step.
Why does the dot product of a and b equal zero? I thought this would only be the case if a and b were at right angles to each other. The solutions seem to be a general proof and should work for all isosceles triangles (not just right angle triangles).
The solution would still make sense even if a · b didn't equal zero. Why does it equal zero here?
Thanks